题目内容

设θ和φ是方程acosx+b sinx=c的二个根，且θ±φ≠2kπ（k∈Z），a、b、c≠0，求证：．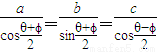
【答案】分析：把θ和φ代入方程，可得两个等式，把它们相减，通过和差化积可得即=；把两等式相加并根据=可得=，进而得证．
解答：解：∵θ和φ是方程acosx+bsinx=c的二个根
∴acosθ+bsinθ=c     ①
acosφ+bsinφ=c       ②
①-②得a（cosθ-cosφ）+b（sinθ-sinφ）=0
∴-2asinsin+2bcossin=sin（bcos-asin）=0
∵θ±φ≠2kπ
∴sin≠0
∴bcos-asin=0，即=③
同理①+②得（acos+bsin）cos=c   ④
把③代入④得=
故．
点评：本题主要考查了三角函数恒等式的证明．证明本题主要是通过和差化积公式完成的．
练习册系列答案
相关题目
设θ和φ是方程acosx+b sinx=c的二个根，且θ±φ≠2kπ（k∈Z），a、b、c≠0，求证：
a
cos
θ+?
2
=
b
sin
θ+?
2
=
c
cos
θ-?
2
．

设和是方程的两个根,则的关系是(   )

A.           B.          

C.           D.

 

已知，设和是方程的两个根，不等式对任意实数恒成立；函数有两个不同的零点.求使“P且Q”为真命题的实数的取值范围.

【解析】本试题主要考查了命题和函数零点的运用。由题设x1＋x2＝a，x1x2＝－2，

∴|x1－x2|＝＝.

当a∈[1,2]时，的最小值为3. 当a∈[1,2]时，的最小值为3.

要使|m－5|≤|x1－x2|对任意实数a∈[1,2]恒成立，只须|m－5|≤3，即2≤m≤8.

由已知，得f(x)＝3x2＋2mx＋m＋＝0的判别式

Δ＝4m2－12(m＋)＝4m2－12m－16>0，

得m<－1或m>4.

可得到要使“P∧Q”为真命题，只需P真Q真即可。

解：由题设x1＋x2＝a，x1x2＝－2，

∴|x1－x2|＝＝.

当a∈[1,2]时，的最小值为3.

要使|m－5|≤|x1－x2|对任意实数a∈[1,2]恒成立，只须|m－5|≤3，即2≤m≤8.

由已知，得f(x)＝3x2＋2mx＋m＋＝0的判别式

Δ＝4m2－12(m＋)＝4m2－12m－16>0，

得m<－1或m>4.

综上，要使“P∧Q”为真命题，只需P真Q真，即

解得实数m的取值范围是(4,8]

 

设和是方程的两个根,则的关系是(   )

A．B．
C．D．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网