题目内容
设函数f(x)=x3+ax2-a2x+1,g(x)=ax2-2x+1,其中实数a≠0.
(Ⅰ)若a>0,求函数f(x)的单调区间;
(Ⅱ)当函数y=f(x)与y=g(x)的图象只有一个公共点且g(x)存在最小值时,记g(x)的最小值为h(a),求h(a)的值域;
(Ⅲ)若f(x)与g(x)在区间(a,a+2)内均为增函数,求a的取值范围.
解:(Ⅰ)∵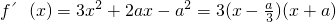 ,又a>0,
,又a>0,
∴当 时,f'(x)>0;
时,f'(x)>0;
当 时,f'(x)<0,
时,f'(x)<0,
∴f(x)在(-∞,-a)和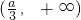 内是增函数,在
内是增函数,在 内是减函数.
内是减函数.
(Ⅱ)由题意知x3+ax2-a2x+1=ax2-2x+1,
即x[x2-(a2-2)]=0恰有一根(含重根).∴a2-2≤0,即 ≤a≤
≤a≤ ,
,
又a≠0,∴ .
.
当a>0时,g(x)才存在最小值,∴ .
.
g(x)=a(x- )2+1-
)2+1- ,
,
∴ .
.
h(a)≤1- ;
;
∴h(a)的值域为 .
.
(Ⅲ)当a>0时,f(x)在(-∞,-a)和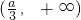 内是增函数,g(x)在
内是增函数,g(x)在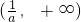 内是增函数.
内是增函数.
由题意得 ,解得a≥1;
,解得a≥1;
当a<0时,f(x)在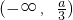 和(-a,+∞)内是增函数,g(x)在
和(-a,+∞)内是增函数,g(x)在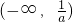 内是增函数.
内是增函数.
由题意得 ,解得a≤-3;
,解得a≤-3;
综上可知,实数a的取值范围为(-∞,-3]∪[1,+∞).
分析:(1)先对函数f(x)进行求导,令导函数大于0可求函数的增区间,令导函数小于0可求函数的减区间.
(2)令f(x)=g(x)整理可得x[x2-(a2-2)]=0,故a2-2≤0求出a的范围,再根据g(x)存在最小值必有a>0,最后求出h(a)的值域即可.
(3)分别求出函数f(x)与g(x)的单调区间,然后令(a,a+2)为二者单调增区间的子集即可.
点评:本题主要考查函数的单调性与其导函数的正负情况之间的关系,即当导函数小于0时原函数单调递减,当导函数大于0时原函数单调递增.
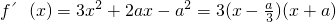 ,又a>0,
,又a>0,∴当
 时,f'(x)>0;
时,f'(x)>0;当
 时,f'(x)<0,
时,f'(x)<0,∴f(x)在(-∞,-a)和
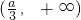 内是增函数,在
内是增函数,在 内是减函数.
内是减函数.(Ⅱ)由题意知x3+ax2-a2x+1=ax2-2x+1,
即x[x2-(a2-2)]=0恰有一根(含重根).∴a2-2≤0,即
 ≤a≤
≤a≤ ,
,又a≠0,∴
 .
.当a>0时,g(x)才存在最小值,∴
 .
.g(x)=a(x-
 )2+1-
)2+1- ,
,∴
 .
.h(a)≤1-
 ;
;∴h(a)的值域为
 .
.(Ⅲ)当a>0时,f(x)在(-∞,-a)和
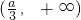 内是增函数,g(x)在
内是增函数,g(x)在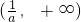 内是增函数.
内是增函数.由题意得
 ,解得a≥1;
,解得a≥1;当a<0时,f(x)在
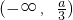 和(-a,+∞)内是增函数,g(x)在
和(-a,+∞)内是增函数,g(x)在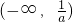 内是增函数.
内是增函数.由题意得
 ,解得a≤-3;
,解得a≤-3;综上可知,实数a的取值范围为(-∞,-3]∪[1,+∞).
分析:(1)先对函数f(x)进行求导,令导函数大于0可求函数的增区间,令导函数小于0可求函数的减区间.
(2)令f(x)=g(x)整理可得x[x2-(a2-2)]=0,故a2-2≤0求出a的范围,再根据g(x)存在最小值必有a>0,最后求出h(a)的值域即可.
(3)分别求出函数f(x)与g(x)的单调区间,然后令(a,a+2)为二者单调增区间的子集即可.
点评:本题主要考查函数的单调性与其导函数的正负情况之间的关系,即当导函数小于0时原函数单调递减,当导函数大于0时原函数单调递增.

练习册系列答案
 春雨教育同步作文系列答案
春雨教育同步作文系列答案
相关题目