题目内容
在△ABC中,若 ,则△ABC是( )
,则△ABC是( )A.等腰三角形
B.直角三角形
C.等腰直角三角形
D.等腰三角形或直角三角形
【答案】分析:利用余弦定理表示出cosB及cosA,变形后代入已知等式的右边,整理后利用正弦定理化简,再利用二倍角的正弦函数公式化简得到sin2A=sin2B,由A和B都为三角形的内角,可得2A与2B相等或2A与2B互补,进而得到A等于B或A与B互余,可得出三角形为等腰三角形或直角三角形.
解答:解:∵cosB=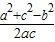 ,cosA=
,cosA=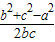 ,
,
∴a2+c2-b2=2ac•cosB,b2+c2-a2=2bc•cosA,
∴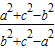 =
=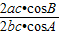 =
=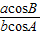 =
=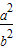 ,又
,又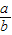 =
=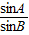 ,
,
∴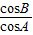 =
=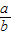 =
=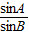 ,即sinAcosA=sinBcosB,
,即sinAcosA=sinBcosB,
∴sin2A=sin2B,又A和B都为三角形的内角,
∴2A=2B或2A+2B=180°,即A=B或A+B=90°,
则△ABC为等腰三角形或直角三角形.
故选D
点评:此题考查了正弦、余弦定理,二倍角的正弦函数公式,以及正弦函数的图象与性质,熟练掌握定理及公式是解本题的关键.
解答:解:∵cosB=
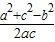 ,cosA=
,cosA=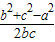 ,
,∴a2+c2-b2=2ac•cosB,b2+c2-a2=2bc•cosA,
∴
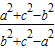 =
=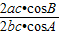 =
=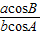 =
=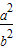 ,又
,又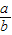 =
=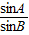 ,
,∴
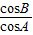 =
=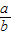 =
=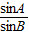 ,即sinAcosA=sinBcosB,
,即sinAcosA=sinBcosB,∴sin2A=sin2B,又A和B都为三角形的内角,
∴2A=2B或2A+2B=180°,即A=B或A+B=90°,
则△ABC为等腰三角形或直角三角形.
故选D
点评:此题考查了正弦、余弦定理,二倍角的正弦函数公式,以及正弦函数的图象与性质,熟练掌握定理及公式是解本题的关键.

练习册系列答案
相关题目
 ,则B的值为( )
,则B的值为( )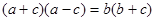 ,则∠A=( )
,则∠A=( ) B.
B. C.
C.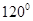 D.
D.
 ,则∠A=
,则∠A= 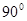 B.
B.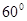 C.
C. D.
D.
 ,
, ,若
,若 ,
, ,则
,则 ()
()  A.
A. B.
B.
 D.
D.
 ,则其面积等于( )
,则其面积等于( ) B.
B. C.1
D.2
C.1
D.2