题目内容
等差数列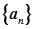 的前
的前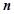 项和记为
项和记为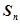 ,已知
,已知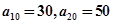 ;
;
(1)求数列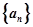 的通项
的通项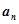
(2)若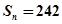 ,求
,求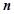
(3)令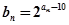 ,求数列
,求数列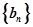 的前
的前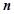 项和
项和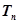
【答案】
(1)2n+10(2) 或
或 (舍去)(3)
(舍去)(3)
【解析】本试题主要是考查了数列的通项公式的求解和数列求和的综合运用
(1)由 ,得方程组
,得方程组
解得首项和公差,得到通项公式。
(2)由 得方程
得方程 ,解方程得到n的值。
,解方程得到n的值。
(3)由(1)得 ,
,
 是首项是4,公比
是首项是4,公比 的等比数列
的等比数列
得到前n项和。
解:(1)由 ,得方程组
,得方程组 ,
,
解得

(2)由 得方程
得方程
解得 或
或 (舍去)
(舍去)
(3)由(1)得 ,
,
 是首项是4,公比
是首项是4,公比 的等比数列
的等比数列
 数列
数列 的前
的前 项和
项和

练习册系列答案
相关题目
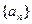 的前
的前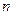 项和记为
项和记为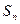
 ,已知
,已知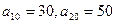 .
.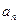 ;
;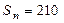 ,求
,求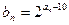 ,求证:数列
,求证:数列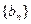 为等比数列.
为等比数列. 的前
的前 项和记为
项和记为 ,已知
,已知
 ;
;  求
求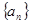 的前
的前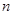 项和记为
项和记为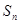 ,已知
,已知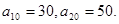
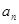 ;
; 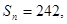 求
求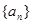 的前
的前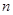 项和记为
项和记为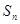 ,已知
,已知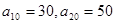 .
.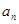 ;
;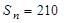 ,求
,求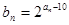 ,求证:数列
,求证:数列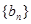 为等比数列.
为等比数列.