题目内容
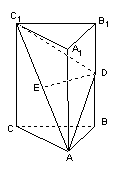 如图,在直三棱柱
如图,在直三棱柱![]() 中,
中,![]() 、
、![]() 分别为
分别为![]() 、
、![]() 的中点。
的中点。
(I)证明:ED为异面直线![]() 与
与![]() 的公垂线;
的公垂线;
(II)设![]() 求二面角
求二面角![]() 的大小。
的大小。
解法一:
(Ⅰ)设O为AC中点,连结EO,BO,则EO![]()
![]() 又
又![]()
![]()
![]() ,所以
,所以![]()
![]()
![]() ,
,
EOBD为平行四边行,ED∥OB。 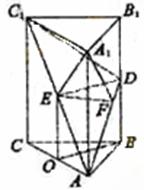
∵AB=BC,∴RO⊥AC,
又平面ABC⊥平面ACC1A1,BO![]() 面ABC,故BO⊥平面ACC1A1,
面ABC,故BO⊥平面ACC1A1,
∴ED⊥平面ACC1A1,ED⊥AC1、ED⊥CC1,
∴ED⊥BB1,ED为异面直线AC1与BB1的公垂线。
(Ⅱ)连结A1E,由AA1=AC=![]() AB可知,A1ACC1为正方形,
AB可知,A1ACC1为正方形,
∴A1E⊥AC1,又由ED⊥平面A1ACC1和ED![]() 平面ADC1知平面ADC1⊥平面A1ACC1,
平面ADC1知平面ADC1⊥平面A1ACC1,
∴A1E⊥平面ADC1,作EF⊥AD,垂足为F,连结A1F,则A1F⊥AD,∠A1FE为二面角![]() 的平面角。
的平面角。
不妨设AA1=2,
则AC=2,AB=![]() ,ED=OB=1,EF=
,ED=OB=1,EF=![]() ,
,![]()
∴∠A1EF=60O。
所以二面角![]() 为60O。
为60O。
解法二:
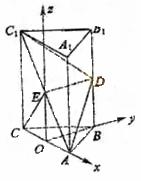
(Ⅰ)如图,建立直角坐标系O-xyz,其中原点O为AC的中点。
设A(a,0,0),B(0,b,0),B1(0,b,2c).
则![]()
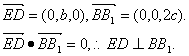
又 ![]()
![]() ∴
∴![]()
所以ED是异面直线BB1与AC1的公垂线。
(Ⅱ)不妨设A(1,0,0)
则B(0,1,0),C(-1,0,0),A(1,0,2),
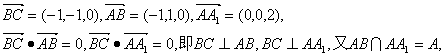
∴ BC⊥面A1AD.
又 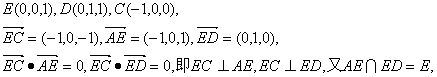
∴ EC⊥面C1AD.
 ,即得
,即得![]() 和
和![]() 的夹角为600
的夹角为600
所以二面角![]() 为60°。
为60°。

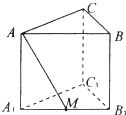 如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1=
如图,在直三棱柱中,∠ACB=90°,AC=BC=1,侧棱AA1= 中, AB=1,
中, AB=1, ,
, .
. ;
; —B的正切值。
—B的正切值。
 中,
中, ,
, 分别为
分别为 的中点,四边形
的中点,四边形 是边长为
是边长为 的正方形.
的正方形. 平面
平面 ;
; 平面
平面 的余弦值.
的余弦值.
 中,
中, ,
, ,
, 是
是 的中点.
的中点. ∥平面
∥平面 ;
; 的余弦值;
的余弦值; 上是否存在点
上是否存在点 ,使
,使 与
与 成
成 角?若存在,确定
角?若存在,确定
 中,
中, ,点
,点 是
是 的中点.
的中点. ;(2)
;(2) 平面
平面 .
.