题目内容
设抛物线![]() :
:![]() 的焦点到准线的距离是
的焦点到准线的距离是![]() .
.
(Ⅰ)求此抛物线方程;
(Ⅱ)设点![]() 在此抛物线上,点
在此抛物线上,点![]() 为此抛物线的焦点,且
为此抛物线的焦点,且![]() ,若
,若![]() ,求直线
,求直线![]() 在
在![]() 轴上截距的取值范围.
轴上截距的取值范围.
解:(Ⅰ)因为抛物线![]() :
:![]() 的焦点到准线的距离
的焦点到准线的距离![]() ……(2分)
……(2分)
所以此抛物线方程为![]() …………(4分)
…………(4分)
(Ⅱ)由题意,直线![]() 的斜率存在.
的斜率存在.![]() ,设直线
,设直线![]() 的方程为
的方程为![]() …(5分)
…(5分)
由 消
消![]() ,整理得,
,整理得,![]() …………(6分)
…………(6分)
![]() ,设
,设![]() ,
,![]() 则
则
![]() ,
,![]() …………(7分)
…………(7分)
因为![]() ,所以
,所以![]() ,于是
,于是 ……(8分)
……(8分)
由![]() ,得
,得![]() ,又
,又![]() ,
,
消![]() 得
得 ![]() ,因为
,因为![]() ,所以
,所以![]() ,从而,
,从而,![]() . …………(10分)
. …………(10分)
代入![]() 得,
得,![]() ,令
,令![]() ,
,
因为![]() 在
在![]() 上递增,所以
上递增,所以![]() ,即
,即
![]() , …………(12分)
, …………(12分)
于是,![]() ,或
,或![]() …………(13分)
…………(13分)
所以直线![]() 在
在![]() 轴上截距的取值范围为
轴上截距的取值范围为![]() . …………(14分)
. …………(14分)

练习册系列答案
相关题目
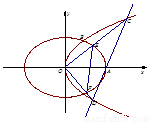
 如图,抛物线
如图,抛物线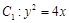 的焦点到准线的距离与椭圆
的焦点到准线的距离与椭圆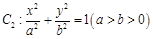 的长半轴相等,设椭圆的右顶点为
的长半轴相等,设椭圆的右顶点为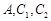 在第一象限的交点为
在第一象限的交点为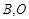 为坐标原点,且
为坐标原点,且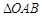 的面积为
的面积为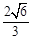
 的标准方程;
的标准方程; 作直线
作直线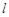 交
交 于
于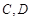 两点,射线
两点,射线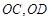 分别交
分别交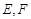 两点.
两点.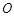 点在以
点在以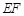 为直径的圆的内部;
为直径的圆的内部;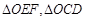 的面积分别为
的面积分别为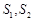 ,问是否存在直线
,问是否存在直线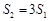 ?请说明理由.
?请说明理由. ,若λ∈[4,9],求直线AB在y轴上截距的取值范围.
,若λ∈[4,9],求直线AB在y轴上截距的取值范围.