题目内容
由x=0,x=
,y=0和y=cosx围成的封闭图形面积是
| 3π | 2 |
3
3
.分析:求由x=0,x=
,y=0和y=cosx围成的封闭图形面积,首先作出余弦函数y=cosx在[0,
]上的图象,
由图象看出封闭图形有两部分构成,x轴上方的部分直接求余弦函数在[0,
]上的定积分,而x轴下方的是余弦函数在[
,
]上定积分的负值.
| 3π |
| 2 |
| 3π |
| 2 |
由图象看出封闭图形有两部分构成,x轴上方的部分直接求余弦函数在[0,
| π |
| 2 |
| π |
| 2 |
| 3π |
| 2 |
解答:解:如图,
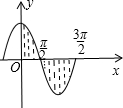
由x=0,x=
,y=0和y=cosx围成的封闭图形面积为:
cosxdx
cosxdx=
=sin
-sin0-(sin
-sin
)=1+2=3.
故答案为3.

由x=0,x=
| 3π |
| 2 |
| ∫ |
0 |
| -∫ |
|
| sinx| |
0 |
| -sinx| |
|
| π |
| 2 |
| 3π |
| 2 |
| π |
| 2 |
故答案为3.
点评:本题考查了定积分,考查了微积分基本定理,曲线在x轴下方所围成的曲边梯形的面积应是函数在区间上定积分的负值,此题为中档题.

练习册系列答案
 黎明文化寒假作业系列答案
黎明文化寒假作业系列答案
相关题目
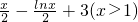 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由;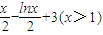 是否是集合M中的元素,并说明理由;
是否是集合M中的元素,并说明理由; .
. 的单调区间;
的单调区间; ,若对任意
,若对任意 ,
, ,不等式
,不等式 恒成立,求实数
恒成立,求实数 的取值范围.
的取值范围. 的定义域是
的定义域是

 得1<x<3;由x>0及
得1<x<3;由x>0及 得0<x<1或x>3,
得0<x<1或x>3, 的单调递增区间是(1,3);单调递减区间是
的单调递增区间是(1,3);单调递减区间是
 不等式
不等式 恒成立,问题等价于
恒成立,问题等价于 只需研究最值即可。
只需研究最值即可。 上,x=1是函数极小值点,这个极小值是唯一的极值点,
上,x=1是函数极小值点,这个极小值是唯一的极值点, ; ............6分
; ............6分
 ;
; 时,
时, ;
; ;
............8分
;
............8分
 ........11分
........11分 或
或  即
即 ,所以实数b的取值范围是
,所以实数b的取值范围是