题目内容
【选修4-5：不等式选讲】
已知函数
（1）求不等式
的解集；
（2）若关于
的不等式
的解集非空，求实数
的取值范围.
解：（Ⅰ）不等式f（x）≤6 即|2x+1|+|2x﹣3|≤6，
∴①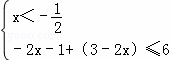
，或②
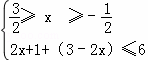，或③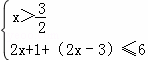
．
解①得﹣1≤x＜﹣
，解②得﹣≤x≤
，解③得 ＜x≤2．
故由不等式可得
，
即不等式的解集为{x|﹣1≤x≤2}．
（Ⅱ）∵f（x）=|2x+1|+|2x﹣3|≥|（2x+1）﹣（2x﹣3）|=4，即f（x）的最小值等于4，
∴|a﹣1|＞4，解此不等式得a＜﹣3或a＞5．
故实数a的取值范围为（﹣∞，﹣3）∪（5，+∞）．
练习册系列答案
相关题目