题目内容
设函数f (x)＝x3－4x＋a，0＜a＜2．若f (x)的三个零点为x1，x2，x3，且x1＜x2＜x3，则
| A．x1＞－1 | B．x2＜0 | C．x2＞0 | D．x3＞2 |
C
解析试题分析：因为函数所以
令
可得
，因为当
时，
，在
上，
，
在
，，故函数在
上是增函数，在上是减函数，在上是增函数.故
是极大值，
是极小值.再由f （x）的三个零点为x1，x2，x3，且x1＜x2＜x3，可得
,
,
.根据
，可得
考点：利用导数研究函数的极值；函数的零点．
点评：本题主要考查函数的零点的定义，函数的零点与方程的根的关系，利用导数研究函数的单调性，利用导数求函数的极值，属于中档题．利用导数研究函数的单调性，利用导数求函数的极值，再根据f （x）的三个零点为x1，x2，x3，且x1＜x2＜x3，求得各个零点所在的区间，从而得出结论．
练习册系列答案
相关题目
设
,用二分法求方程
内近似解的过程中得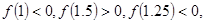
则方程的根落在区间（ ）
A． | B． | C． | D．不能确定 |
下列说法中
① 若定义在R上的函数
满足
，则6为函数的周期；
② 若对于任意
，不等式
恒成立，则
；
③ 定义：“若函数对于任意
R，都存在正常数
，使
恒成立，则称函数为有界泛函．”由该定义可知，函数
为有界泛函；
④对于函数
设
，
，…，
（
且
），令集合
，则集合为空集.正确的个数为
| A．1个 | B．2个 | C．3个 | D．4个 |
已知单位向量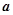
、
，满足
，则函数
（
）
| A．既是奇函数又是偶函数 | B．既不是奇函数也不是偶函数 |
| C．是偶函数 | D．是奇函数 |
函数y=log
x+log2x2+2的值域是（ ）
| A．（0,+∞） | B．[1,+∞) | C．（1,+∞） | D．R |
的图象的是
由表格中的数据可以判定方程
的一个零点所在的区间是
，则
的值为
 | -1 | 0 | 1 | 2 | 3 |
 | 0.37 | 1 | 2.72 | 7.39 | 20.09 |
 | 1 | 2 | 3 | 4 | 5 |
（ ）
对于函数
，若存在
,使
成立，则称
为的不动点. 已知函数
，若对任意实数b，函数恒有两个相异的不动点，则实数
的取值范围是 （ ）
| A．(0,1) | B．（1，+∞） | C．［0，1) | D．以上都不对 |