题目内容
过双曲线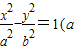
＞0，b＞0）的左焦点F1的直线y=
（x+c）与双曲线的右支交于点P，若sin∠F1OP=
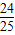（O为坐标原点），则双曲线的离心率是（ ）A．
B．5
C．
D．
【答案】分析：过P点作PA⊥x轴，由此求出PA，OA的值，利用P在直线y=
（x+c）上，可求OF，利用双曲线的定义求出a的值，从而问题得解．
解答：解：过P点作PA⊥x轴，设PA=24k
∵sin∠FOP=
，∴sin∠POA=
，∴OP=25k，∴OA=7k
∵P在直线y=
（x+c）上，∴24k=
（7k+c），∴c=25k，即OF=25k，∴FA=32k，∴PF=40k
∵OF=OF1 =25k，∴AF1=18k，∴PF1=30k
∵2a=PF-PF1=40k-30k=10k，∴a=5k，∴e=
，
故选B．
点评：本题主要考查椭圆的性质，关键是找出几何量a，c的关系，属于基础题．
（x+c）上，可求OF，利用双曲线的定义求出a的值，从而问题得解．解答：解：过P点作PA⊥x轴，设PA=24k
∵sin∠FOP=
，∴sin∠POA=，∴OP=25k，∴OA=7k ∵P在直线y=
（x+c）上，∴24k=（7k+c），∴c=25k，即OF=25k，∴FA=32k，∴PF=40k∵OF=OF1 =25k，∴AF1=18k，∴PF1=30k
∵2a=PF-PF1=40k-30k=10k，∴a=5k，∴e=
，故选B．
点评：本题主要考查椭圆的性质，关键是找出几何量a，c的关系，属于基础题．
练习册系列答案
相关题目
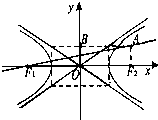如图，已知双曲线E：
(a＞0,b＞0)的左焦点且垂直于x轴的直线与双曲线相交于M、N两点,以MN为直径的圆恰好过双曲线的右顶点,则双曲线的离心率为________.
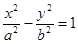(a>0, b>0)的右焦点F作圆
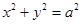的切线FM(切点为M), 交y轴于点P. 若M为线段FP的中点,
则双曲线的离心率是 （
）
B.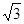
C.2 D.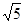
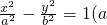＞0，b＞0）的左焦点F1的直线y=
（x+c）与双曲线的右支交于点P，若sin∠F1OP=
（O为坐标原点），则双曲线的离心率是
