Question

已知函数f(x)=log_ax和g(x)=2log_a(2x+t-2)，(a＞0，a≠1，t∈R)的图像在x=2处的切线互相平行.

(Ⅰ)求t的值；

(Ⅱ)设F(x)=g(x)-f(x)，当x∈[1，4]时，F(x)≥2恒成立，求a的取值范围.

Answer 1

解：(Ⅰ)∵f′(x)=log_ae,g′(x)=log_ae 

∵函数f(x)和g(x)的图像在x=2处的切线互相平行∴f′(2)=g′(2) 

∴log_ae=log_ae  ∴t=6

(Ⅱ)∵t=6∴F(x)=g(x)-f(x)=2log_a(2x+4)-log_ax=log_a,x∈[1,4]

令h(x)=4-=4x++16,x∈[1,4]

∵h′(x)=4-=,x∈[1,4]

∴当1≤x＜2时,h′(x)＜0,当2＜x≤4时,h′(x)＞0.

∴h(x)在[1,2)是单调减函数,在(2,4]是单调增函数.

∴h(x)_min=h(2)=32,∴h(x)_max=h(1)=h(4)=36

∴当0＜a＜1时,有F(x)_min=log_a36,当a＞1时,有F(x)_min=log_a32.

∵当x∈[1,4]时,F(x)≥2恒成立,∴F(x)_min≥2 

∴满足条件的a的值满足下列不等式组

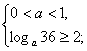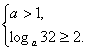  ①,或   ②

不等式组①的解集为空集,解不等式组②得1＜a≤

综上所述,满足条件的a的取值范围是：1＜a≤.