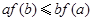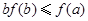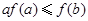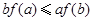题目内容
设f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),则f(- )= ( )
)= ( )
A.- B.-
B.- C .
C . D.
D. 
 )= ( )
)= ( )A.-
 B.-
B.- C .
C . D.
D. 
A
试题分析:解:∵f(x)是周期为2的奇函数,当0≤x≤1时,f(x)=2x(1-x),∴根据周期性可知,f(-
 )=f(-
)=f(- ),再利用奇函数性质可知 f(-
),再利用奇函数性质可知 f(- )=-f(
)=-f( )=-
)=- ,故答案为:A.
,故答案为:A.点评:本题考查函数的周期性和奇偶性的应用,以及求函数的值.

练习册系列答案
相关题目
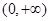 ,若对给定的正数K,定义
,若对给定的正数K,定义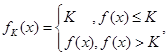 则当函数
则当函数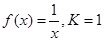 时,
时, 
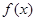 ,在使
,在使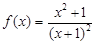 的下确界为_______________.
的下确界为_______________. 在R上可导,且满足不等式
在R上可导,且满足不等式 恒成立,且常数
恒成立,且常数 满足
满足 ,则下列不等式一定成立的是( )
,则下列不等式一定成立的是( )



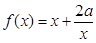
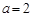 ,证明函数
,证明函数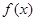 在
在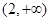 上单调递增;
上单调递增;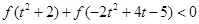 .
.
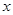 的不等式
的不等式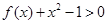
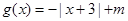 ,
,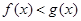 的解集非空,求实数m的取值范围
的解集非空,求实数m的取值范围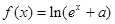 (
(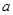 为常数,
为常数,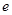 是自然对数的底数)是实数集
是自然对数的底数)是实数集 上的奇函数.
上的奇函数.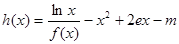 的零点的个数.
的零点的个数.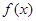 是定义在
是定义在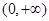 上的非负可导函数,且满足
上的非负可导函数,且满足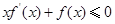 ,对任意正数
,对任意正数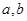 ,若
,若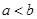 ,则必有( )
,则必有( )