题目内容
已知函数y=f（x）（x∈R）满足f（x+2）=2f（x），且x∈[-1，1]时，f（x）=-|x|+1，则当x∈（0，10]时，y=f（x）与g（x）=log4x的图象的交点个数为（ ）
| A、11 | B、10 | C、9 | D、8 |
分析：利用条件作出函数y=f（x）与g（x）=log4x的图象，利用图象得到函数的交点个数即可．
解答：解：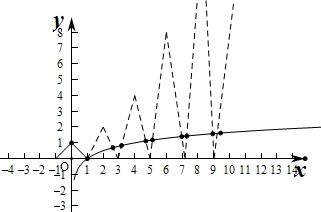
∵y=f（x）（x∈R）满足f（x+2）=2f（x），且x∈[-1，1]时，f（x）=-|x|+1，
∴（x）=
，
分别作出函数y=f（x）与g（x）=log4x的图象如图：
由图象可知y=f（x）与g（x）=log4x的图象的交点个数为9个．
故选：C．
∵y=f（x）（x∈R）满足f（x+2）=2f（x），且x∈[-1，1]时，f（x）=-|x|+1，∴（x）=
|
分别作出函数y=f（x）与g（x）=log4x的图象如图：
由图象可知y=f（x）与g（x）=log4x的图象的交点个数为9个．
故选：C．
点评：本题主要考查函数图象的交点个数问题，利用条件求出函数f（x）的表达式，然后利用数形结合是解决本题的关键．
练习册系列答案
相关题目
已知函数y=f（x）是定义在R上的奇函数，当x＞0 时，f（x）的图象如图所示，则不等式x[f（x）-f（-x）]≤0 的解集为
已知函数y=f（x）的图象如图，则满足