题目内容
已知函数f（x）=lg（x+1），g（x）=lg（1-x）．（1）求函数f（x）-g（x）的定义域；
（2）判断函数f（x）-g（x）的奇偶性，并说明理由；
（3）判断函数f（x）-g（x）在定义域上的单调性，并证明你的结论．
【答案】分析：（1）利用真数大于0，可得函数的定义域；
（2）利用奇偶函数的定义，可得函数f（x）-g（x）的奇偶性；
（3）利用函数单调性的定义，可得函数f（x）-g（x）在定义域上的单调性．
解答：解：（1）由x+1＞0且1-x＞0，得-1＜x＜1，因此函数定义域为{x|-1＜x＜1}；
（2）设F（x）=f（x）-g（x），则F（-x）=f（-x）-g（-x）=lg（-x+1）-lg（1+x）=-F（x），
∴F（x）=f（x）-g（x）是奇函数；
（3）函数f（x）-g（x）在定义域上为增函数．
设f（x）-g（x）=lg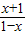
，令h（x）=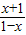
设-1＜x1＜x2＜1，则h（x1）-h（x2）=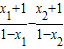
=
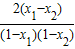
∵-1＜x1＜x2＜1，∴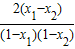
＜0，∴h（x1）-h（x2）＜0，
∴h（x） 在（-1，1）上为增函数，
∴f（x）-g（x）在（-1，1）上为增函数．
点评：本题考查函数的单调性与奇偶性，掌握函数奇偶性与单调性的定义是关键．
（2）利用奇偶函数的定义，可得函数f（x）-g（x）的奇偶性；
（3）利用函数单调性的定义，可得函数f（x）-g（x）在定义域上的单调性．
解答：解：（1）由x+1＞0且1-x＞0，得-1＜x＜1，因此函数定义域为{x|-1＜x＜1}；
（2）设F（x）=f（x）-g（x），则F（-x）=f（-x）-g（-x）=lg（-x+1）-lg（1+x）=-F（x），
∴F（x）=f（x）-g（x）是奇函数；
（3）函数f（x）-g（x）在定义域上为增函数．
设f（x）-g（x）=lg
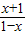，令h（x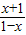）=设-1＜x1＜x2＜1，则h（x1）-h（x2）=
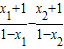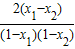
=∵-1＜x1＜x2＜1，∴
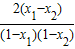＜0，∴h（x1）-h（x2）＜0，∴h（x） 在（-1，1）上为增函数，
∴f（x）-g（x）在（-1，1）上为增函数．
点评：本题考查函数的单调性与奇偶性，掌握函数奇偶性与单调性的定义是关键．
练习册系列答案
相关题目