题目内容
如图,多面体ABC-A1B1C1中,三角形ABC是边长为4的正三角形,AA1∥BB1∥CC1,AA1⊥平面ABC,AA1=BB1=2CC1=4。
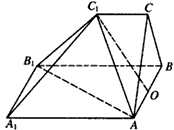
(1)若O是AB的中点,求证:OC⊥A1B;
(2)在线段AB1上是否存在一点D,使得CD∥平面A1B1C1,若存在确定点D的位置;若不存在,说明理由。
(2)在线段AB1上是否存在一点D,使得CD∥平面A1B1C1,若存在确定点D的位置;若不存在,说明理由。
解:(1)设线段A1B1的中点为E,
由AA1⊥平面ABC得AA1⊥AB,
又BB1∥AA1,
所以AA1B1B是正方形,点O是线段AB的中点,
所以OE∥AA1,
所以OE⊥A1B1,
由AA1⊥平面ABC得AA1⊥AC,
又BB1∥AA1∥CC1,
所以BB1⊥BC,CC1⊥AC,CC1⊥BC
且AC=4,AA1=4,CC1=2,
所以A1C1=B1C1,
所以C1E⊥A1B1,
所以A1B1⊥平面DC1E,
所以OC1⊥A1B1。
(Ⅱ)设OE∩AB1=D,则点D是AB1的中点,
所以ED∥AA1,
从而ED∥CC1,ED=CC1、
所以四边形CC1ED是平行四边形,
所以CD∥C1E,
所以CD∥平面A1B1C1,
即存在点D使得CD∥平面A1B1C1,点D是AB1的中点。
由AA1⊥平面ABC得AA1⊥AB,
又BB1∥AA1,
所以AA1B1B是正方形,点O是线段AB的中点,
所以OE∥AA1,
所以OE⊥A1B1,
由AA1⊥平面ABC得AA1⊥AC,
又BB1∥AA1∥CC1,
所以BB1⊥BC,CC1⊥AC,CC1⊥BC
且AC=4,AA1=4,CC1=2,
所以A1C1=B1C1,
所以C1E⊥A1B1,
所以A1B1⊥平面DC1E,
所以OC1⊥A1B1。
(Ⅱ)设OE∩AB1=D,则点D是AB1的中点,
所以ED∥AA1,

从而ED∥CC1,ED=CC1、
所以四边形CC1ED是平行四边形,
所以CD∥C1E,
所以CD∥平面A1B1C1,
即存在点D使得CD∥平面A1B1C1,点D是AB1的中点。

练习册系列答案
 口算心算速算应用题系列答案
口算心算速算应用题系列答案 同步拓展阅读系列答案
同步拓展阅读系列答案
相关题目
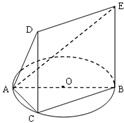 如图,多面体ABCDE的一个面ABC内接于圆O,AB是圆O的直径,四边形BCDE为平行四边形,且CD⊥平面ABC.
如图,多面体ABCDE的一个面ABC内接于圆O,AB是圆O的直径,四边形BCDE为平行四边形,且CD⊥平面ABC.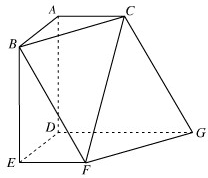 如图,多面体ABCDEFG中,AB,AC,AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1.
如图,多面体ABCDEFG中,AB,AC,AD两两垂直,平面ABC∥平面DEFG,平面BEF∥平面ADGC,AB=AD=DG=2,AC=EF=1. (2013•丰台区二模)如图,多面体EDABC中,AC,BC,CE两两垂直,AD∥CE,ED⊥DC,
(2013•丰台区二模)如图,多面体EDABC中,AC,BC,CE两两垂直,AD∥CE,ED⊥DC,