题目内容
已知等差数列{an}的前n项和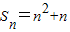 ,则an= .
,则an= .
【答案】分析:由数列{an}的前n项和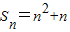 ,分类写出n=1和n≥2时的an,然后验证n≥2时的通项公式是否满足a1.
,分类写出n=1和n≥2时的an,然后验证n≥2时的通项公式是否满足a1.
解答:解:因为数列{an}的前n项和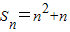 ,
,
当n=1时,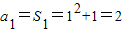 ,
,
当n≥2时,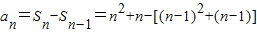 =2n.
=2n.
验证n≥2时的式子对n=1时成立,所以,an=2n.
所以,等差数列{an}的通项公式为an=2n.
故答案为2n.
点评:本题考查了等差数列的通项公式,考查了由数列的前n项和求数列的通项,该类问题解答时一定要分类讨论,然后加以验证,当a1满足n≥2时的通项时,通项公式合并在一起写,否则要分写,此题是基础题.
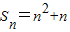 ,分类写出n=1和n≥2时的an,然后验证n≥2时的通项公式是否满足a1.
,分类写出n=1和n≥2时的an,然后验证n≥2时的通项公式是否满足a1.解答:解:因为数列{an}的前n项和
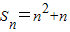 ,
,当n=1时,
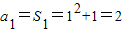 ,
,当n≥2时,
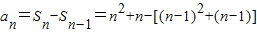 =2n.
=2n.验证n≥2时的式子对n=1时成立,所以,an=2n.
所以,等差数列{an}的通项公式为an=2n.
故答案为2n.
点评:本题考查了等差数列的通项公式,考查了由数列的前n项和求数列的通项,该类问题解答时一定要分类讨论,然后加以验证,当a1满足n≥2时的通项时,通项公式合并在一起写,否则要分写,此题是基础题.

练习册系列答案
 高中必刷题系列答案
高中必刷题系列答案
相关题目
 已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.
已知等差数列{an}中,a4a6=-4,a2+a8=0,n∈N*.