题目内容
已知正项数列{an},其前n项和Sn满足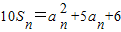 ,
,(1)求证:数列{an}是等差数列;
(2)若a1,a3,a15成等比数列,求数列{an}的通项an.
【答案】分析:(1)由已知中前n项和Sn满足10Sn=an2+5an+6,根据an=Sn-Sn-1,可以得到an与an-1的差为定值,进而根据等差数列的定义得到答案;
(2)结合a1,a3,a15成等比数列,令n=1,我们可以求出a1,分类讨论后,即可得到满足条件的a1及an与an-1的关系,进而求出数列{an}的通项an.
解答:证明:(1)∵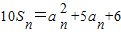 …①
…①
∴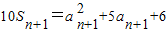 …②
…②
②-①得:
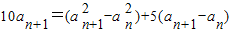
即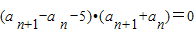
∵数列{an}为正项数列
∴(an+1+an)≠0
∴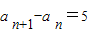
即数列{an}是等差数列
(2)当n=1时,
解得a1=2,或a1=3
由(1)得等差数列{an}的公差d=5,
当a1=3时,a3=13,a15=73. a1,a3,a15不成等比数列
∴a1≠3;
当a1=2时,a3=12,a15=72,有 a32=a1a15,
∴a1=2,
∴an=5n-3.
点评:本题考查的知识点是数列的通项公式,数列的函数特征,其中在已知中包含有Sn的表达式,求通项an时,an=Sn-Sn-1(n≥2)是最常用的办法.
(2)结合a1,a3,a15成等比数列,令n=1,我们可以求出a1,分类讨论后,即可得到满足条件的a1及an与an-1的关系,进而求出数列{an}的通项an.
解答:证明:(1)∵
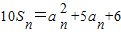 …①
…①∴
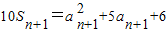 …②
…②②-①得:
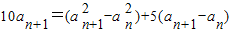
即
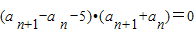
∵数列{an}为正项数列
∴(an+1+an)≠0
∴
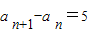
即数列{an}是等差数列
(2)当n=1时,

解得a1=2,或a1=3
由(1)得等差数列{an}的公差d=5,
当a1=3时,a3=13,a15=73. a1,a3,a15不成等比数列
∴a1≠3;
当a1=2时,a3=12,a15=72,有 a32=a1a15,
∴a1=2,
∴an=5n-3.
点评:本题考查的知识点是数列的通项公式,数列的函数特征,其中在已知中包含有Sn的表达式,求通项an时,an=Sn-Sn-1(n≥2)是最常用的办法.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目