题目内容
如图正方体ABCD-A1B1C1D1中，E，F分别为AB，CC1的中点，则异面直线A1C与EF所成角的余弦值为（ ）A、
| ||||
B、
| ||||
C、
| ||||
D、
|
分析：因为是正方体，又是求空间角，所以易选用向量法，先建立如图所示坐标系，再求得相应点的坐标，相关向量的坐标，最后用向量的夹角公式求解．
解答：
解：建立如图所示空间直角坐标：设正方体的棱长为2
则A1（2，0，2），C（0，2，0），E（2，1，0），F（0，2，1）
∴
=(-2，2，-2)，
=(-2，1，1)
∴cos＜
，
＞ =
故选B
解：建立如图所示空间直角坐标：设正方体的棱长为2则A1（2，0，2），C（0，2，0），E（2，1，0），F（0，2，1）
∴
| A1C |
| EF |
∴cos＜
| A1E |
| EF |
| ||
| 3 |
故选B
点评：本题主要考查多面体的结构特征及空间角的求法，同时，还考查了转化思想和运算能力，属中档题．
练习册系列答案
相关题目
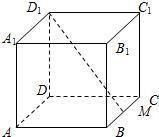如图正方体ABCD-A1B1C1D1中，M为BC中点，则直线D1M与平面ABCD所成角的正切值为
如图正方体ABCD-A1B1C1D1的棱长为1，点M是棱AA1的中点，点O是BD1的中点，求证：OM是异面直线AA1，BD1的公垂线，并求OM的长．
如图正方体ABCD-A1B1C1D1的棱长为2，则点B1到直线AC的距离是
（文）如图正方体ABCD-A1B1C1D1，在它的12条棱及12条面的对角线所在的直线中，选取若干条直线确定平面，在所有的这些平面中：
甲．如图1，平面VAD⊥平面ABCD，△VAD是等边三角形，ABCD是矩形，AB：AD=