Question

已知函数f(x)=，在x=1处取得极值为2.

（1）求函数f(x)的解析式；

（2）若函数f(x)在区间（m，2m＋1）上为增函数，求实数m的取值范围；

（3）若P（x₀，y₀）为f(x)=图象上的任意一点，直线l与f(x)=的图象相切于点P，求直线l的斜率的取值范围.

Answer 1

解：（1）已知函数f(x)=，

∴f′(x)=,

又函数f(x)在x=1处取得极值2，

∴即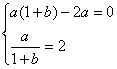

∴f(x)=.

（2）∵f′(x)==.

由f′(x)＞0，得4-4x²＞0，即-1＜x＜1,

所以f(x)= 的单调增区间为（-1，1）.

因函数f(x)在（m，2m＋1）上单调递增，则有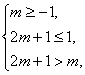解得-1＜m≤0，

即m∈(-1,0)时，函数f(x)在（m，2m＋1）上为增函数.

（3）f(x)=,

∴f′(x)=,

直线l的斜率为k=f′(x₀)=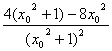=4［］.

令=t，t∈(0,1),则直线l的斜率k=4(2t²-t),t∈(0,1)

∴k∈［-,4］，即直线l的斜率k的取值范围是［-,4］

［或者由k=f′(x₀)转化为关于x₀²的方程，根据该方程有非负根求解］.