题目内容
已知函数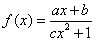 (a,b,c为常数,a≠0),
(a,b,c为常数,a≠0),
(Ⅰ)若c=0时,数列{an}满足条件:点(n,an)在函数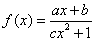 的图象上,求{an}的前n项和
的图象上,求{an}的前n项和
Sn;
(Ⅱ)在(Ⅰ)的条件下,若a3=7,S4=24,p,q∈N*(p≠q),证明: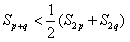 ;
;
(Ⅲ)若c=1时,f(x)是奇函数,f(1)=1,数列{xn}满足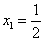 ,xn+1= f(xn),求证:
,xn+1= f(xn),求证:
 。
。
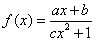 (a,b,c为常数,a≠0),
(a,b,c为常数,a≠0),(Ⅰ)若c=0时,数列{an}满足条件:点(n,an)在函数
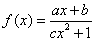 的图象上,求{an}的前n项和
的图象上,求{an}的前n项和Sn;
(Ⅱ)在(Ⅰ)的条件下,若a3=7,S4=24,p,q∈N*(p≠q),证明:
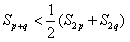 ;
;(Ⅲ)若c=1时,f(x)是奇函数,f(1)=1,数列{xn}满足
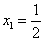 ,xn+1= f(xn),求证:
,xn+1= f(xn),求证: 。
。(Ⅰ)解:依条件有f(x)=ax+b,
因为点 在函数f(x)=ax+b的图象上,所以
在函数f(x)=ax+b的图象上,所以 ,
,
因为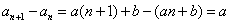 ,
,
所以{an}是首项是 ,公差为d=a的等差数列,
,公差为d=a的等差数列,
所以 ,
,
即数列{an}的前n项和 。
。
(Ⅱ)证明:依条件有 ,即
,即 解得
解得 ,
,
所以 ,
,
所以 ,
,
因为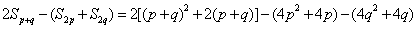
 ,
,
又p≠q,
所以 ,
,
即 。
。
(Ⅲ)证明:依条件 ,
,
因为f(x)为奇函数,所以f(-x)+f(x)=0,
即 ,解得b=0,
,解得b=0,
所以 ,
,
又f(1)=1,所以a=2,
故 ;
;
因为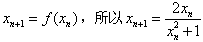 ,
,
所以 (n∈N*),
(n∈N*),
又 ,
,
若 矛盾,
矛盾,
所以 ,
,
所以 ,
,
所以 ,
,
所以

 ,
,
因为 ,
,
所以 ,
,
所以 。
。
因为点
 在函数f(x)=ax+b的图象上,所以
在函数f(x)=ax+b的图象上,所以 ,
,因为
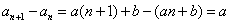 ,
,所以{an}是首项是
 ,公差为d=a的等差数列,
,公差为d=a的等差数列,所以
 ,
,即数列{an}的前n项和
 。
。(Ⅱ)证明:依条件有
 ,即
,即 解得
解得 ,
,所以
 ,
,所以
 ,
,因为
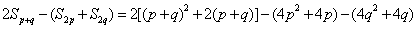
 ,
,又p≠q,
所以
 ,
,即
 。
。(Ⅲ)证明:依条件
 ,
,因为f(x)为奇函数,所以f(-x)+f(x)=0,
即
 ,解得b=0,
,解得b=0,所以
 ,
,又f(1)=1,所以a=2,
故
 ;
;因为
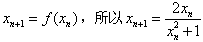 ,
,所以
 (n∈N*),
(n∈N*),又
 ,
,若
 矛盾,
矛盾,所以
 ,
,所以
 ,
,所以
 ,
,所以


 ,
,因为
 ,
,所以
 ,
,所以
 。
。
练习册系列答案
相关题目
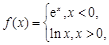 则
则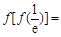 ( )
( )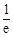 B.
B.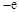 C.
C.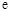 D.
D. (a,b,c∈N),且f(2)=2,f(3)<3,
(a,b,c∈N),且f(2)=2,f(3)<3,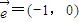 平移后得到的图象关于原点对称.
平移后得到的图象关于原点对称.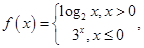 则
则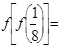 ( )
( )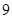 B.
B.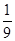 C.
C.
 D.
D.
 已知函数
已知函数  若
若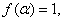
 =
=