题目内容
若函数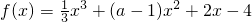
的导函数f'（x）在区间（-∞，4]上是减函数，则实数a的取值范围是
- A.（-∞，-3）
- B.（-∞，-3]
- C.（-3，+∞）
- D.[-3，+∞）
B
分析：先求出原函数的导数，再根据导函数f'（x）在区间（-∞，4]上是减函数，转化为f'′（x）≤0在（-∞，4]上恒成立，列出关于a的不等关系解之即得．
解答：f'（x）=x2+2（a-1）x+2，
则f∥（x）=2x+2（a-1）≤0在（-∞，4]上恒成立，
∴8+2（a-1）≤0，∴a≤-3，
故选B．
点评：本小题主要考查函数单调性的应用、利用导数研究函数的单调性、不等式的解法等基础知识，考查运算求解能力、化归思想．属于基础题．
分析：先求出原函数的导数，再根据导函数f'（x）在区间（-∞，4]上是减函数，转化为f'′（x）≤0在（-∞，4]上恒成立，列出关于a的不等关系解之即得．
解答：f'（x）=x2+2（a-1）x+2，
则f∥（x）=2x+2（a-1）≤0在（-∞，4]上恒成立，
∴8+2（a-1）≤0，∴a≤-3，
故选B．
点评：本小题主要考查函数单调性的应用、利用导数研究函数的单调性、不等式的解法等基础知识，考查运算求解能力、化归思想．属于基础题．
练习册系列答案
名校通行证有效作业系列答案
相关题目
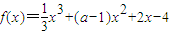的导函数f'（x）在区间（-∞，4]上是减函数，则实数a的取值范围是（ ）
的导函数f'（x）在区间（-∞，4]上是减函数，则实数a的取值范围是（ ）