题目内容
 (2012•眉山一模)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CA=CB=CC1=2,M是BC的中点.
(2012•眉山一模)如图,在直三棱柱ABC-A1B1C1中,∠ACB=90°,CA=CB=CC1=2,M是BC的中点.(I)求证:A1C∥平面AB1M;
(Ⅱ)求二面角B-AB1-M的大小;
(Ⅲ)求点C1到平面AB1M的距离.
分析:(I)证明线面平行,通常利用线面平行的判定定理,这里我们可以利用中位线的性质,得到线线平行;
(Ⅱ)先作出二面角的平面角,再进行求解,过点M作MN⊥AB于N,连接ON,可证∠MON是二面角B-AB1-M的平面角,在直角△OMN中,可求二面角B-AB1-M的大小;
(Ⅲ)设点C1到平面AB1M的距离为d,利用VC1-AB1M=VA-C1B1M,可求点C1到平面AB1M的距离.
(Ⅱ)先作出二面角的平面角,再进行求解,过点M作MN⊥AB于N,连接ON,可证∠MON是二面角B-AB1-M的平面角,在直角△OMN中,可求二面角B-AB1-M的大小;
(Ⅲ)设点C1到平面AB1M的距离为d,利用VC1-AB1M=VA-C1B1M,可求点C1到平面AB1M的距离.
解答: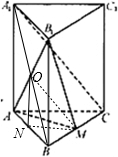 (I)证明:连接A1B,交AB1于O,连接OM
(I)证明:连接A1B,交AB1于O,连接OM
因为直三棱柱ABC-A1B1C1,所以O是A1B的中点
因为O,M分别是A1B和BC的中点,所以OM∥A1C
因为A1C?面AB1M,OM?面AB1M
所以A1C∥面AB1M
(Ⅱ)解:过点M作MN⊥AB于N,连接ON
∵平面ABC⊥平面ABB1A1,
∴MN⊥平面ABB1A1,可知ON是OM在平面ABB1A1内的射影
又O是A1B的中点,则OM⊥A1B,∴AB1⊥ON
故∠MON是二面角B-AB1-M的平面角
∵CA=2,∴B1M=
,AM=
,AB1=2
∴OM=
,MN=
在直角△OMN中,sin∠MON=
=
=
∴二面角B-AB1-M的大小为30°;
(Ⅲ)解:设点C1到平面AB1M的距离为d,由VC1-AB1M=VA-C1B1M得
×(
×2
×
)d=
×(
×2×2)×2.
∴d=
∴点C1到平面AB1M的距离为
 (I)证明:连接A1B,交AB1于O,连接OM
(I)证明:连接A1B,交AB1于O,连接OM 因为直三棱柱ABC-A1B1C1,所以O是A1B的中点
因为O,M分别是A1B和BC的中点,所以OM∥A1C
因为A1C?面AB1M,OM?面AB1M
所以A1C∥面AB1M
(Ⅱ)解:过点M作MN⊥AB于N,连接ON
∵平面ABC⊥平面ABB1A1,
∴MN⊥平面ABB1A1,可知ON是OM在平面ABB1A1内的射影
又O是A1B的中点,则OM⊥A1B,∴AB1⊥ON
故∠MON是二面角B-AB1-M的平面角
∵CA=2,∴B1M=
| 5 |
| 5 |
| 3 |
∴OM=
| 2 |
| ||
| 2 |
在直角△OMN中,sin∠MON=
| MN |
| OM |
| ||||
|
| 1 |
| 2 |
∴二面角B-AB1-M的大小为30°;
(Ⅲ)解:设点C1到平面AB1M的距离为d,由VC1-AB1M=VA-C1B1M得
| 1 |
| 3 |
| 1 |
| 2 |
| 3 |
| 2 |
| 1 |
| 3 |
| 1 |
| 2 |
∴d=
2
| ||
| 3 |
∴点C1到平面AB1M的距离为
2
| ||
| 3 |
点评:证明线面平行,通常运用线面平行的判定定理,求面面角遵循:作证求的步骤,利用等体积,可解决点到面的距离问题.

练习册系列答案
相关题目