题目内容
设函数y=Ax3+bx2+Cx+D的图象与y轴交点为P点,且曲线在P点处的切线方程为12x-y-4=0.若函数在x=2处取得极值0,试确定函数的解析式.
解:∵y=ax3+bx2+cx+d的图象与y轴的交点为P,
∴P的坐标为P(0,d).
又曲线在点P处的切线方程为y=12x-4,P点坐标适合方程,
从而D=-4.
又切线斜率k=12,
故在x=0处的导数y′|x=0=12,
而y′=3ax2+2bx+C,y′|x=0=c,
从而c=12.又函数在x=2处取得极值0,所以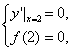
即![]()
解得A=2,b=-9.
∴所求函数解析式为y=2x3-9x2+12x-4.

练习册系列答案
相关题目