题目内容
函数y=sin2x的最小正周期T=
π
π
.分析:先利用降幂公式把y=sin2x化简为y=
cos2x+
,因为函数y=Acos(ωx+∅)+h的周期为
,把ω的值代入即可.
| 1 |
| 2 |
| 1 |
| 2 |
| 2π |
| w |
解答:解:y=sin2x可变形为y=
=
cos2x+
,
∴最小正周期T=
=π
故答案为π
| 1-cos2x |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
∴最小正周期T=
| 2π |
| 2 |
故答案为π
点评:本题主要考查应用降幂公式化简三角函数式,以及y=Acos(ωx+∅)+h类型函数的周期的求法.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
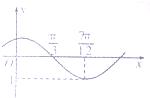 (2013•蚌埠二模)已知函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<
(2013•蚌埠二模)已知函数f(x)=Asin(ωx+φ)(其中A>0,|φ|<