题目内容
已知抛物线y2=2px(p>0),若有过动点M(a,0)且斜率为1的直线l与抛物线交于不同两点A、B,|AB|≤2p.(1)求a的取值范围;(2)若线段AB的垂直平分线交x轴于点N,求△NAB面积的最大值.
思路解析:设出A、B两点的坐标,则得 解:(1)设A( 又直线l的斜率为1,∴y2-y1= ∴| 由0<|AB|≤2p可得- (2)设AB的垂直平分线交AB于点Q(x,y),则 x= ∵| ∴△NAB的最大面积为
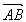 ,(1)即求证|
,(1)即求证|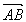 |≤2p;(2)若AB的垂直平分线交AB于Q,则可得
|≤2p;(2)若AB的垂直平分线交AB于Q,则可得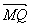 、
、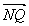 结合三角形面积公式易求.
结合三角形面积公式易求. ![]() ,y1),B(
,y1),B(![]() ,y2),则
,y2),则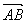 =(
=(![]() ,y2-y1),
,y2-y1),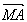 =(
=(![]() -a,y1),
-a,y1),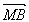 =(
=(![]() -a,y2). ∵
-a,y2). ∵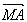 与
与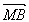 共线,∴(
共线,∴(![]() -a)y2-(
-a)y2-(![]() -a)y1=0
-a)y1=0![]() y1y2=-2pa.
y1y2=-2pa.![]()
![]() y1+y2=2p.
y1+y2=2p.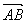 |=
|=![]() |y2-y1|=
|y2-y1|=![]() =
=![]() .
.![]() <a≤-
<a≤-![]() .
.![]() =a+p,y=
=a+p,y=![]() =p,∴
=p,∴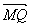 =(p,p),|
=(p,p),|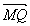 |=
|=![]() p(定值).
p(定值).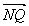 |=|
|=|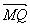 |,∴S△NAB=
|,∴S△NAB=![]() |
|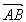 |·|
|·|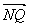 |=
|=![]() p·|
p·|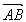 |≤
|≤![]() p2.
p2.![]() p2.
p2.
 练习册系列答案
练习册系列答案
经纶学典江苏13大市中考试卷汇编四色卷系列答案
金榜之路中考总复习中考全真模拟封闭卷系列答案
亮点激活高分宝典系列答案
天利38套对接高考单元专题训练系列答案
最新3年中考利剑中考试卷汇编系列答案
考进名校系列答案
北京市重点城区3年真题2年模拟试卷系列答案
河南省重点中学模拟试卷精选及详解系列答案
成都中考真题精选系列答案
名校密卷四川名校招生真卷60套系列答案
相关题目