题目内容
如图所示,已知A(0,a),B(0,b)且a＞b＞0,P在x轴正半轴上,求∠APB的最大值及此时点P的坐标.
解：设P（x,0）(x＞0),∠APB=θ,则θ是直线AP与BP的夹角.
∴kPA=-
,kPB=-
,0＜θ＜
.∴tanθ=|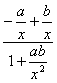
|=
=
.
∵a＞b＞0,x＞0,∴x+
≥2
,当且仅当x=
,即x=
时取等号.
∴0＜tanθ≤
,此时θ=arctan
,即当且仅当P(
,0)时，∠APB取最大值
arctan
.
练习册系列答案
相关题目
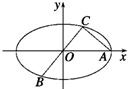如图所示，已知A，B，C是椭圆
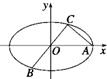如图所示，已知A、B、C是椭圆E：
如图所示，已知A（4，0）、B（0，4），从点P（2，0）射出的光线经直线AB反射后再射到直线OB上，最后经直线OB反射后又回到P点，则光线所经过的路程是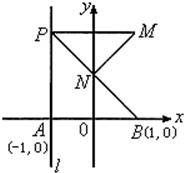
（2007•崇文区二模）如图所示，已知A（-1，0），B（1，0），直线l垂直AB于A点，P为l上一动点，点N为线段BP上一点，且满足