题目内容
设p=(log2x)2+(t-2)log2x-t+1,若t在区间[-2,2]上变动时,p恒为正值,试求x的取值范围.分析:根据题意,对p化简可得p=(log2x-1)t+(log2x)2-2log2x+1,因为t∈[-2,2]时p恒为正值,所以把t=-2和t=2两个数代入p=(log2x-1)t+(log2x)2-2log2x+1中,令p都大于0,由此得到一个不等式组,解这个不等式组就能得到答案.
解答:解:p=(log2x-1)t+(log2x)2-2log2x+1,∵t∈[-2,2]时p恒为正值,
∴
解得log2x<-1或log2x>3,
即0<x<
或x>8.
∴
|
解得log2x<-1或log2x>3,
即0<x<
| 1 |
| 2 |
点评:充分控掘题设中的隐含条件,恰当地建立不等式组是准确解题的关键.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
设p:log2x<0,q:(
)x-1>1,则p是q的( )
| 1 |
| 2 |
| A、充要条件 |
| B、充分不必要条件 |
| C、必要不充分条件 |
| D、既不充分也不必要条件 |
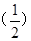 x-1>1,则p是q的 ( ).
x-1>1,则p是q的 ( ).