题目内容
设函数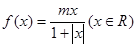 ,区间
,区间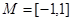 ,集合
,集合 ,则使
,则使 成立的实数
成立的实数 的个数为
的个数为
| A.1 | B.2 | C.3 | D.无数 |
B
解析试题分析:先判断函数f(x)是奇函数,题意可得,当-1≤x≤1时,函数的值域为[-1,1].分m>0和m<0 两种情况,分别利用函数的单调性求得m的值,综合可得结论。根据题意,函数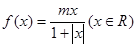 ,可得
,可得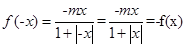 ,故为奇函数,同时
,故为奇函数,同时
题意可得,当-1≤x≤1时,函数的值域为[-1,1].①若x∈[0,1],且m>0,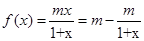
故函数在[0,1]上是增函数,故函数f(x)在区间M=[-1,1]上是增函数,故有f(-1)=-1,f(1)=1,即 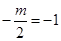 ,解得 m=2.
,解得 m=2.
②若x∈[0,1],且m<0,由 f(x)=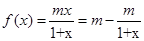 ,故函数在[0,1]上是减函数,故函数f(x)在区间M=[-1,1]上是减函数,故有f(-1)=1,f(1)=-1,即
,故函数在[0,1]上是减函数,故函数f(x)在区间M=[-1,1]上是减函数,故有f(-1)=1,f(1)=-1,即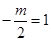 解得 m=-2.
解得 m=-2.
③显然,m=0不满足条件.
综上可得,m=±2,故使M=N成立的实数m的个数为2,
故选B.
考点:函数奇偶性以及参数范围
点评:本题主要考查集合关系中参数的取值范围问题,函数的奇偶性、单调性的应用,体现了分类讨论的数学思想,属于基础题.

练习册系列答案
相关题目
已知集合 ,
, ,在集合
,在集合 中任取一个元素
中任取一个元素 ,则 “
,则 “ ”的概率是
”的概率是
A. | B. | C. | D. |
以下六个关系式:① ,②
,② ,③
,③ , ④
, ④ , ⑤
, ⑤ ,⑥
,⑥ 是空集,其中错误的个数是 ( )
是空集,其中错误的个数是 ( )
| A.4 | B.3 | C.2 | D.1 |
设集合 ,
, ,则
,则 ( )
( )
A. | B. | C. | D. |
函数 设
设
 ﹒﹒﹒
﹒﹒﹒ (
( ,N≥2),令集合M={x∣
,N≥2),令集合M={x∣ }则集合M为( )
}则集合M为( )
A. | B.实数集 | C.单元素集 | D.二元素集 |
下列各数集及对应法则,不能构成映射的是 ( )
A. , , , , |
B. , , , , |
C. , , , , |
D. , , , , |
设U=R,若集合 ,则CUA等于( )
,则CUA等于( )
A. | B. |
C. | D. |
对于集合 和
和 ,定义
,定义 ,
,

 ,设
,设 ,
, ,则
,则
A. | B. | C. | D. |
已知集合U={1,2,3,4,5,6},A={1,,4,5},B={2,3,4},则 =
=
| A.{4}, | B.U={1,5}, | C.U={1,5,6}, | D.U={1,4,5,6} |