题目内容
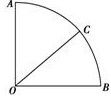
如图,在圆心角为90°的扇形中,以圆心O为起点作射线OC,求使得∠AOC 和∠BOC都不小于30°的概率 .
考点:
几何概型.
专题:
计算题.
分析:
本题可选用面积计算概率,作∠AOD=∠BOE=30°,分别求扇形AOB、DOE的面积,也可从角度考虑,同时也可利用弧DE的长度是弧AB长度的.选用“测度”为角度计算更加简洁.
解答:
解:记事件A=“作射线OC,使∠AOC 和∠BOC都不小于30°”;
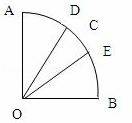
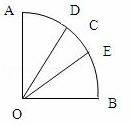
作射线OD、OE,使∠AOD=∠BOE=30°,
当OC在∠DOE内时,∠AOC 和∠BOC都不小于30°,
则:P=![]() .
.
故答案为:![]() .
.
点评:
解决几何概型的求概率问题,关键是构造出随机事件对应的几何图形,利用几何图形的几何度量来求随机事件的概率.变换测度,一题多解,同时选用不同的“测度”有时可简化解题.

练习册系列答案
相关题目
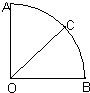 如图,在圆心角为90°的扇形中以圆心O为起点作射线OC,则使得∠AOC与∠BOC都不小于30°的概率是( )
如图,在圆心角为90°的扇形中以圆心O为起点作射线OC,则使得∠AOC与∠BOC都不小于30°的概率是( )A、
| ||
B、
| ||
C、
| ||
D、
|
 如图,在圆心角为90°的扇形中,以圆心O为起点作射线OC,求使得∠AOC和∠BOC都不小于30°的概率.
如图,在圆心角为90°的扇形中,以圆心O为起点作射线OC,求使得∠AOC和∠BOC都不小于30°的概率.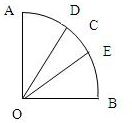 如图,在圆心角为90°的扇形中,以圆心O为起点作射线OC,求使得∠AOC 和∠BOC都不小于30°的概率
如图,在圆心角为90°的扇形中,以圆心O为起点作射线OC,求使得∠AOC 和∠BOC都不小于30°的概率
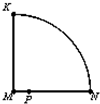 如图,在圆心角为90°的扇形MNK中,动点P从点M出发,沿MN→
如图,在圆心角为90°的扇形MNK中,动点P从点M出发,沿MN→