题目内容
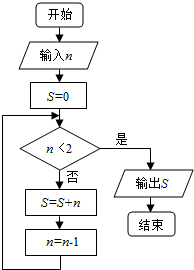
10.设函数f(x)=-4x+a,不等式|f(x)|<6的解集为(-1,2)(1)求a的值;
(2)解不等式$\frac{4x+m}{f(x)}$>0(m∈R).
分析 (1)不等式|f(x)|<6,化为结合不等式-6<f(x)<6的解集为{x|-1<x<2}.我们可以构造关于a的方程组,解方程组即可得到a的值;
(2)由于不等式中含有参数m,故我们要对参数m进行分类讨论,分m=-2,m>-2,m<-2三种情况进行讨论,最后综合讨论结果即可得到答案
解答 解:(1)∵|f(x)|<6的解集为(-1,2)
∴$\left\{\begin{array}{l}{\frac{1}{4}(a-6)=-1}\\{\frac{1}{4}(a+6)=2}\end{array}\right.$,解得a=2
(2)由式$\frac{4x+m}{f(x)}$=$\frac{4x+m}{-4x+2}$>0得(x-$\frac{1}{2}$)(x+$\frac{m}{4}$)<0,
①当-$\frac{m}{4}$>$\frac{1}{2}$,即m<-2时,$\frac{1}{2}$<x<-$\frac{m}{4}$
②当-$\frac{m}{4}$=$\frac{1}{2}$,即m=-2时,无解
③当-$\frac{m}{4}$<$\frac{1}{2}$,即m>-2时,-$\frac{m}{4}$<x<$\frac{1}{2}$,
∴当m<-2时,解集为($\frac{1}{2}$,-$\frac{m}{4}$)
当m=-2时,解集为空集
当m>-2时,解集为(-$\frac{m}{4}$,$\frac{1}{2}$).
点评 本题考查的知识点是绝对值不等式的解法,一元二次不等式的应用,在(2)中关键是对参数m分m=-2,m>-2,m<-2三种情况进行讨论.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目
20.若a,b,c∈(0,+∞),且a+b+c=1,则$\frac{1}{a+b}$+$\frac{1}{b+c}$+$\frac{1}{c+a}$的最小值为( )
| A. | $\frac{1}{3}$ | B. | $\frac{\root{3}{2}}{3}$ | C. | $\frac{9}{2}$ | D. | $\frac{1}{9}$ |
15.cos(-2640°)+sin1665°=( )
| A. | $\frac{{1+\sqrt{3}}}{2}$ | B. | -$\frac{{1+\sqrt{3}}}{2}$ | C. | $\frac{{1+\sqrt{2}}}{2}$ | D. | -$\frac{{1+\sqrt{2}}}{2}$ |
2.不等式(3x+1)(2x-1)>0的解集是( )
| A. | $\{x|x<-\frac{1}{3}或x>\frac{1}{2}\}$ | B. | $\{x|-\frac{1}{3}<x<\frac{1}{2}\}$ | C. | $\{x|x>\frac{1}{2}\}$ | D. | $\{x|x>-\frac{1}{3}\}$ |
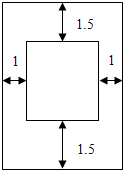 某出版社出版一读物,为了排版设计的需要,规定:一页上所印文字的矩形区域需要占去150cm2,上、下边各要留1.5cm宽的空白,左、右两边各要留1cm宽的空白,出版商为了节约纸张,应选用怎样尺寸的矩形纸张来设计版面?
某出版社出版一读物,为了排版设计的需要,规定:一页上所印文字的矩形区域需要占去150cm2,上、下边各要留1.5cm宽的空白,左、右两边各要留1cm宽的空白,出版商为了节约纸张,应选用怎样尺寸的矩形纸张来设计版面?