题目内容
若集合A={a,0,-1},B={c+b,
,1},且A=B,f(x)=ax2+bx+c.
(1)求a,b,c的值
(2)作出函数y=|f(x)|的大致图象,并指出其增区间.
| 1 | b+a |
(1)求a,b,c的值
(2)作出函数y=|f(x)|的大致图象,并指出其增区间.
分析:(1)根据集合相等的概念,可构造关于a,b,c的方程,解方程可得a,b,c的值
(2)由(1)可得函数y=|f(x)|的解析式,进而根据二次函数的图象和性质画出草图,分析出函数的单调递增区间
(2)由(1)可得函数y=|f(x)|的解析式,进而根据二次函数的图象和性质画出草图,分析出函数的单调递增区间
解答:解:(1)∵A=B,
∴
,
∴
,
(2)由(1)得f(x)=x2-2x+2=(x-1)2+1>0恒成立,
∴y=|f(x)|=x2-2x+2
其图象是开口朝上且以直线x=1为对称轴的抛物线,如下图所示:
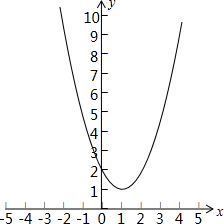
故函数的单调递增区间为[1,+∞)
∴
|
∴
|
(2)由(1)得f(x)=x2-2x+2=(x-1)2+1>0恒成立,
∴y=|f(x)|=x2-2x+2
其图象是开口朝上且以直线x=1为对称轴的抛物线,如下图所示:
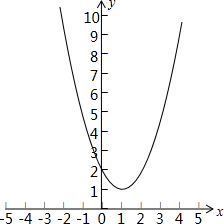
故函数的单调递增区间为[1,+∞)
点评:本题考查的知识点是函数图象的作法,待定系数法求函数的解析式,二次函数的图象和性质,是函数的简单综合应用,难度不大.

练习册系列答案
相关题目
若集合A={y|y≥0},A∪B=B,则集合B不可能是( )
A、{y|y=
| ||
| B、{y|y=lgx,x>0} | ||
C、{y|y=(
| ||
| D、∅ |