题目内容
已知二次函数 与两坐标轴分别交于不同的三点A、B、C.
与两坐标轴分别交于不同的三点A、B、C.
(1)求实数t的取值范围;
(2)当 时,求经过A、B、C三点的圆F的方程;
时,求经过A、B、C三点的圆F的方程;
(3)过原点作两条相互垂直的直线分别交圆F于M、N、P、Q四点,求四边形 的面积的最大值。
的面积的最大值。
【答案】
(1)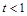 且
且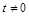 ;(2)圆F的方程为
;(2)圆F的方程为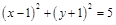 ;(3)四边形
;(3)四边形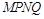 的面积的最大值为
的面积的最大值为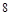 .
.
【解析】
试题分析:(1)利用一元二次方程根的判别式易求得结果;(2)当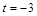 时,
时,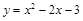 ,分别令
,分别令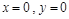 得二次函数与两坐标轴的三个不同交点坐标,再设圆的一般方程或标准方程利用待定系数法求得圆的方程;(3)画出图形,利用垂径定理和勾股定理表示
得二次函数与两坐标轴的三个不同交点坐标,再设圆的一般方程或标准方程利用待定系数法求得圆的方程;(3)画出图形,利用垂径定理和勾股定理表示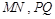 ,列出面积函数,利用均值不等式求四边形
,列出面积函数,利用均值不等式求四边形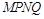 的面积的最大值.
的面积的最大值.
试题解析:(1)由已知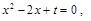 由
由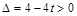 及
及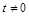 ,得
,得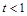 且
且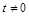 .
4分
.
4分
(2)当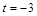 时,
时,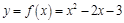 ,分别令
,分别令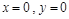 得二次函数与两坐标轴的三个不同交点坐标
得二次函数与两坐标轴的三个不同交点坐标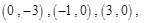 设圆F的方程为
设圆F的方程为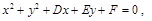 则
则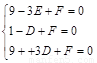 ,解得
,解得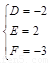 ,所以圆
,所以圆 的方程为
的方程为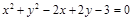 ,即
,即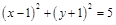 .
8分
.
8分
(3)如图: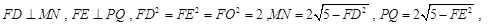
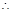 四边形
四边形 的面积
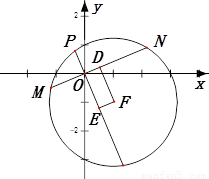
的面积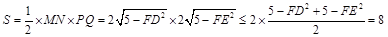 .
.
 四边形
四边形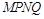 的面积的最大值为
的面积的最大值为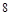 .
14分
.
14分
考点:1、直线与抛物线位置关系;2、圆的方程的求法;3、解析几何最值问题.

练习册系列答案
相关题目
 、B
、B 、C
、C 三点,过坐标原点O的直线
三点,过坐标原点O的直线 与抛物线交于M、N两点.分别过点C、D
与抛物线交于M、N两点.分别过点C、D 作平行于
作平行于 轴的直线
轴的直线 、
、 .(1)求抛物线对应的二次函数的解析式;
.(1)求抛物线对应的二次函数的解析式; 表示),并证明M、N两
表示),并证明M、N两