题目内容
已知A(2,0),B(0,2),C(cosα,sinα),且α∈(0,π).
(1)若|
+
|=
,求
与
的夹角的余弦值.
(2)若
⊥
,求tanα的值.
(1)若|
| OA |
| OC |
| 7 |
| OB |
| OC |
(2)若
| AC |
| BC |
分析:(1)由|
+
|=
得出cosα与sinα所满足的条件,将其代入
与
的夹角的余弦公式中求出余弦值即可.
(2)两向量垂直,则它们的内积为0,由此建立关于cosα,sinα的方程由此方程结合同角三角函数的关系求出正切值即可.
| OA |
| OC |
| 7 |
| OB |
| OC |
(2)两向量垂直,则它们的内积为0,由此建立关于cosα,sinα的方程由此方程结合同角三角函数的关系求出正切值即可.
解答:解:(1)∵由|
+
|=
,A(2,0),B(0,2),C(cosα,sinα),
∴(2+cosα)2+sin2α=7,解得cosα=
与
的夹角的余弦值为
=
=sinα=
=
与
的夹角的余弦值是
(2)∵
⊥
∴
•
=0又
=(cosα-2,sinα),
=(cosα,sinα-2),
∴cos2α-2cosα+sin2α-2sinα=0
即cosα+sinα=
即1+2cosαsinα=
即
=-
,解得tanα=-
又由cosα+sinα=
及向量夹角的取取值范围知,α是个钝角且正弦的绝对值大于余弦的绝对值
故tanα=-
| OA |
| OC |
| 7 |
∴(2+cosα)2+sin2α=7,解得cosα=
| 1 |
| 2 |
| OB |
| OC |
| ||||
|
|
| 2sinα |
| 2 |
| 1-cos2α |
| ||
| 2 |
| OB |
| OC |
| ||
| 2 |
(2)∵
| AC |
| BC |
∴
| AC |
| BC |
| AC |
| BC |
∴cos2α-2cosα+sin2α-2sinα=0
即cosα+sinα=
| 1 |
| 2 |
即1+2cosαsinα=
| 1 |
| 4 |
即
| tanα |
| 1+tan 2α |
| 3 |
| 8 |
4±
| ||
| 3 |
又由cosα+sinα=
| 1 |
| 2 |
故tanα=-
4+
| ||
| 3 |
点评:本题考查数量积表示两个向量的夹角以及三角函数的恒等变换及化简求值,求解此类题的关键是正确应用公式时行变形,以及正确运算,莫因马虎算错导致前功尽弃.

练习册系列答案
相关题目
已知A(2,0),B(3,3),直线l⊥AB,则直线l的斜率k=( )
| A、-3 | ||
| B、3 | ||
C、-
| ||
D、
|
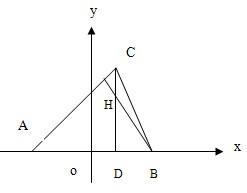 如图,在△ABC中,已知A(-
如图,在△ABC中,已知A(- 如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且
如图,已知A(-2,0),B(2,0),等腰梯形ABCD满足|AB|=-2|CD|,E为AC上一点,且