已知函数f(x)=x3+ax2+bx+a2.在x=1处有极值10．的解析式,+16x-4.讨论函数g(x)的单调性．题目和参考答案——青夏教育精英家教网—

题目内容

已知函数f(x)=x³+ax²+bx+a²，在x=1处有极值10．

(1)求f(x)的解析式；

(2)令g(x)=f(x)+16x-4，讨论函数g(x)的单调性．

解：(1)f′(x)=3x2+2ax+b．

由题意可得：

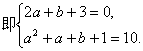
解得或

但a=-3，b=3时，f′(x)=3x²-6x+3=3(x-1)²，

f′(x)在x=1的两侧附近符号相同，∴f(x)在x=1处不取得极值．

∴a=4，b=-11．

∵f(x)=x³+4x²-11x+16．

(2)g(x)=x³+4x²+5x+12．

令g′(x)=3x²+8x+5=0，得x₁=，x₂=-1．

列表如下

x	(-∞,)		(,-1)	-1	(-1,+∞)
g′(x)	+	0	-	0	+
g(x)		极大值		极小值

从而g(x)的递增区间是(-∞， )和(-1，+∞)，递减区间是(，-1).

练习册系列答案

（2011•上海模拟）已知函数f(x)=(

-1)2+(

-1)2，x∈(0，+∞)，其中0＜a＜b．
（1）当a=1，b=2时，求f（x）的最小值；
（2）若f（a）≥2^m-1对任意0＜a＜b恒成立，求实数m的取值范围；
（3）设k、c＞0，当a=k²，b=（k+c）²时，记f（x）=f₁（x）；当a=（k+c）²，b=（k+2c）²时，记f（x）=f₂（x）．
求证：f1(x)+f2(x)＞

4c2

k(k+c)

．

已知函数f(x)的图像在[a，b]上连续不断，f₁(x)＝min{f(t)|a≤t≤x}(x∈[a，b])，f₂(x)＝max{f(t)|a≤t≤x}(x∈[a，b])，其中，min{f(x)|x∈D}表示函数f(x)在D上的最小值，max{f(x)|x∈D}表示函数f(x)在D上的最大值，若存在最小正整数k，使得f₂(x)－f₁(x)≤k(x－a)对任意的x∈[a，b]成立，则称函数f(x)为[a，b]上的“k阶收缩函数”．已知函数f(x)＝x²，x∈[－1，4]为[－1，4]上的“k阶收缩函数”，则k的值是_________．

已知函数f（x）、g（x），下列说法正确的是（）
A．f（x）是奇函数，g（x）是奇函数，则f（x）+g（x）是奇函数
B．f（x）是偶函数，g（x）是偶函数，则f（x）+g（x）是偶函数
C．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）一定是奇函数或偶函数
D．f（x）是奇函数，g（x）是偶函数，则f（x）+g（x）可以是奇函数或偶函数

试题分类