题目内容
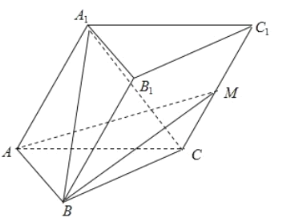
【题目】如图,三棱锥![]() 的侧棱长都相等,底面
的侧棱长都相等,底面![]() 与侧面
与侧面![]() 都是以
都是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,![]() 为线段
为线段![]() 的中点,
的中点,![]() 为直线
为直线![]() 上的动点,若平面
上的动点,若平面![]() 与平面
与平面![]() 所成锐二面角的平面角为
所成锐二面角的平面角为![]() ,则
,则![]() 的最大值是( )
的最大值是( )
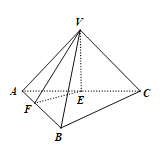
A.![]() B.
B.![]() C.
C.![]() D.
D.![]()
【答案】D
【解析】
连接![]() ,以
,以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,建立空间直角坐标系,求出平面
轴,建立空间直角坐标系,求出平面![]() 的一个法向量
的一个法向量![]() ,平面
,平面![]() 的一个法向量
的一个法向量![]() ,利用
,利用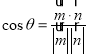 即可求解.
即可求解.
底面![]() 与侧面
与侧面![]() 都是以
都是以![]() 为斜边的等腰直角三角形,
为斜边的等腰直角三角形,
则![]() ,所以
,所以![]()
设![]() ,
,
由![]() 为线段
为线段![]() 的中点,
的中点,
则![]() ,
,
由![]() ,
,
所以![]() ,
,
以![]() 为原点,
为原点,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,![]() 为
为![]() 轴,
轴,
建立空间直角坐标系,如图所示:
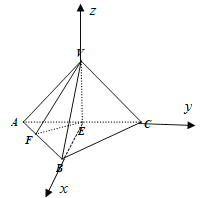
则![]() ,
,![]() ,
,![]() ,设
,设![]() ,
,
![]() ,
,![]() ,
,![]() ,
,![]() ,
,
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则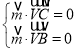 ,即
,即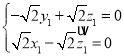 ,
,
令![]() ,则
,则![]() ,
,![]() ,
,
所以![]() .
.
设平面![]() 的一个法向量
的一个法向量![]() ,
,
则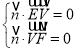 ,即
,即 ,
,
解得![]() ,令
,令![]() ,则
,则![]() ,
,
所以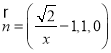 ,
,
平面![]() 与平面
与平面![]() 所成锐二面角的平面角为
所成锐二面角的平面角为![]() ,
,
则 ,
,
将分子、分母同除以![]() ,可得
,可得
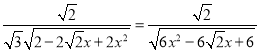
令 ,
,
当![]() 时,
时,![]() ,
,
则![]() 的最大值为:
的最大值为:![]() .
.
故选:D

练习册系列答案
 津桥教育计算小状元系列答案
津桥教育计算小状元系列答案
相关题目