题目内容
椭圆 (a>b>0)的左、右焦点分别为F1、F2,P是椭圆上一点,l为左准线,PQ⊥l,垂足为Q,若四边形PQF1F2为平行四边形,则椭圆的离心率取值范围是
(a>b>0)的左、右焦点分别为F1、F2,P是椭圆上一点,l为左准线,PQ⊥l,垂足为Q,若四边形PQF1F2为平行四边形,则椭圆的离心率取值范围是
- A.(0,
 )
) - B.(0,
 )
) - C.(
 ,1)
,1) - D.(
 ,1)
,1)
C
分析:椭圆上动点P横坐标满足:-a≤x≤a,结合PQF1F2是平行四边形,得|PQ|=|F1F2|=2c=x+ ,所以x=2c-
,所以x=2c- ,由此建立关于ac的不等式,解之再结合椭圆离心率的取值范围,可求得该椭圆的离心率取值范围.
,由此建立关于ac的不等式,解之再结合椭圆离心率的取值范围,可求得该椭圆的离心率取值范围.
解答: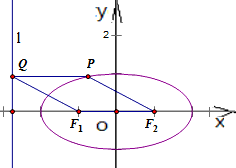 根据题意,得
根据题意,得
∵点P是椭圆上的动点
∴P点横坐标x满足:-a≤x≤a(等号不能成立)
∵四边形PQF1F2为平行四边形,
∴|PQ|=|F1F2|=2c
∵左准线方程为x=- ,|PQ|=x+
,|PQ|=x+ =2c,∴x=2c-
=2c,∴x=2c-
因此可得-a<2c- <a,各项都除以a,得-1<2e-
<a,各项都除以a,得-1<2e- <1
<1
解不等式,得 <e<1
<e<1
故选C
点评:本题给出椭圆上存在动点到左准线的距离等于焦距,求椭圆离心率取值范围,着重考查了椭圆的标准方程和基本概念,椭圆的简单几何性质等知识,属于基础题.
分析:椭圆上动点P横坐标满足:-a≤x≤a,结合PQF1F2是平行四边形,得|PQ|=|F1F2|=2c=x+
 ,所以x=2c-
,所以x=2c- ,由此建立关于ac的不等式,解之再结合椭圆离心率的取值范围,可求得该椭圆的离心率取值范围.
,由此建立关于ac的不等式,解之再结合椭圆离心率的取值范围,可求得该椭圆的离心率取值范围.解答:
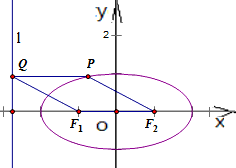 根据题意,得
根据题意,得∵点P是椭圆上的动点
∴P点横坐标x满足:-a≤x≤a(等号不能成立)
∵四边形PQF1F2为平行四边形,
∴|PQ|=|F1F2|=2c
∵左准线方程为x=-
 ,|PQ|=x+
,|PQ|=x+ =2c,∴x=2c-
=2c,∴x=2c-
因此可得-a<2c-
 <a,各项都除以a,得-1<2e-
<a,各项都除以a,得-1<2e- <1
<1解不等式,得
 <e<1
<e<1故选C
点评:本题给出椭圆上存在动点到左准线的距离等于焦距,求椭圆离心率取值范围,着重考查了椭圆的标准方程和基本概念,椭圆的简单几何性质等知识,属于基础题.

练习册系列答案
 名牌学校分层周周测系列答案
名牌学校分层周周测系列答案 黄冈海淀全程培优测试卷系列答案
黄冈海淀全程培优测试卷系列答案
相关题目
 (a>b>0)的离心率e=
(a>b>0)的离心率e= ,连接椭圆的四个顶点得到的菱形的面积为4.
,连接椭圆的四个顶点得到的菱形的面积为4.
 ,求直线l的倾斜角;
,求直线l的倾斜角; 在线段AB的垂直平分线上,且
在线段AB的垂直平分线上,且 .求
.求 的值.
的值. (a>b>0)的右焦点为F2(3,0),离心率为
(a>b>0)的右焦点为F2(3,0),离心率为 .
. (a>b>0)的焦距为4,且与椭圆
(a>b>0)的焦距为4,且与椭圆 有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B.
有相同的离心率,斜率为k的直线l经过点M(0,1),与椭圆C交于不同两点A、B. (a>b>0)的左,右焦点,若椭圆的右准线上存在一点P,使得线段PF1的垂直平分线过点F2,则离心率的范围是 .
(a>b>0)的左,右焦点,若椭圆的右准线上存在一点P,使得线段PF1的垂直平分线过点F2,则离心率的范围是 . 分)
分) (a>b>0)的离心率
(a>b>0)的离心率 ,焦距是函数
,焦距是函数 的零点.
的零点. 与椭圆交于
与椭圆交于 、
、 两点,
两点, ,求k的值.
,求k的值.