Question

已知等比数列{a_n}的前n项和S_n=2ⁿ-a，n∈N^*．设公差不为零的等差数列{b_n}满足：b₁=a₁+2，且b₂+5，b₄+5，b₈+5成等比．
（Ⅰ） 求a及b_n；
（Ⅱ） 设数列{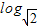a_n}的前n项和为T_n．求使T_n＞b_n的最小正整数n的值．

Answer 1

【答案】分析：（Ⅰ）由等比数列{a_n}的前n项和S_n=2ⁿ-a，n∈N^*，先分别求出a₁，a₂，a₃，由，能求出a；由公差不为零的等差数列{b_n}满足：b₁=a₁+2，且b₂+5，b₄+5，b₈+5成等比数列，列方程组先求出首项和公差，由此能求出b_n．
（Ⅱ）由，知a_n==2（n-1），故数列{a_n}的前n项和T_n=n（n-1）．由此能求出使T_n＞b_n的最小正整数n的值．
解答：解：（Ⅰ）∵等比数列{a_n}的前n项和S_n=2ⁿ-a，n∈N^*，
∴a₁=S₁=2-a，
a₂=（2²-a）-（2-a）=2，
a₃=（2³-a）-（2²-a）=4，
∵，
∴2²=（2-a）•4，解得a=1，
∴．
∵公差不为零的等差数列{b_n}满足：b₁=a₁+2，且b₂+5，b₄+5，b₈+5成等比数列，
∴，
∴（8+3d）²=（8+d）（8+7d），
解得d=0（舍），或d=8，
∴b_n=8n-5，n∈N^*．
（Ⅱ）∵，∴a_n==2（n-1），
∴数列{a_n}的前n项和
T_n=2（1-1）+2（2-1）=2（3-1）+2（4-1）+…+2（n-1）
=2[0+1+2+3+…+（n-1）]
=2×
=n（n-1）．
∵b_n=8n-5，T_n＞b_n，
∴n（n-1）＞8n-5，
∵n∈N^*，∴n≥9，
∴使T_n＞b_n的最小正整数n的值是9．
点评：本题主要考查等差、等比数列的概念，通项公式及求和公式等基础知识，同时考查运算求解能力．