题目内容
平面上的点
使关于t的二次方程
的根都是绝对值不超过1的实数，那么这样的点
的集合在平面内的区域的形状是（ ）
D
解析试题分析：设关于t的二次方程的根为
.由于根的值都是绝对值不超过1的实数， 
由韦达定理可得
.通过作图可知x,y符合D选项的图形.
考点：1.线性规划问题.2.绝对值的知识.
练习册系列答案
快捷英语周周练系列答案
相关题目
设变量
满足
，则
的最大值和最小值分别为（ ）
| A．1，-1 | B．2，-2 | C．1，-2 | D．2，-1 |
是平面区域
内的动点，点
，O为坐标原点，设
的最小值为
，若
恒成立,则实数
的取值范围是（ ）
实数
满足条件
,则
的最小值为( )
| A．16 | B．4 | C．1 | D． |
在平面直角坐标系xOy中，
为不等式组
所表示的区域上一动点，则
的最小值为（ ）
A． | B． | C．1 | D．2 |
若实数
满足
，则
的取值范围是( )
A． | B． | C． | D． |
设
，在约束条件
下，目标函数
的最大值小于2，则
的取值范围为（ ）
A． | B． | C． | D． |
设x、y满足
则
( )
| A．有最小值2，最大值3 |
| B．有最小值2，无最大值 |
| C．有最小值3，无最大值 |
| D．既无最小值，也无最大值 |
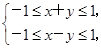则点(x，y)在圆面x2＋y2≤
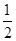内部的概率为( )
