题目内容
(本题满分14分)已知正四棱锥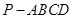 的底面边长为
的底面边长为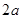 ,
,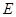 为
为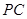 中点.
中点.
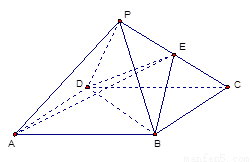
(Ⅰ)求证: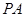 //平面
//平面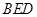 ;
;
(Ⅱ)若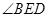 是二面角
是二面角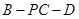 的平面角,求直线
的平面角,求直线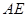 与平面
与平面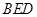 所成角的余弦值.
所成角的余弦值.
【答案】
(Ⅰ)见解析;(Ⅱ)直线 与平面
与平面 所成角的余弦值为
所成角的余弦值为
【解析】本题主要考查立体几何线面平行、直线与平面所成的角和二面角,同时考查空间想象能力和推理论证能力.
(1)利用线面平行的判定定理可以证明该结论。
(2)而线面角的求解可以运用三垂线制作出角,然后借助于直角三角形求解得到结论。
(Ⅰ)解:连结 与
与 交于点
交于点 ,连结
,连结 .
.
 又
又 平面
平面 ,
, 平面
平面 .
.
 平面
平面 .
.
(Ⅱ)解: 是二面角
是二面角 的平面角,
的平面角,
 ,
,
 平面
平面 ,
,
取 中点
中点 ,连结
,连结 ,交
,交 于点
于点 ,则
,则 ,
,
又 侧棱长为
侧棱长为
 平面
平面 ,
,

 就是直线
就是直线 与平面
与平面 所成的角.
所成的角.
又 则
则



故直线 与平面
与平面 所成角的余弦值为
所成角的余弦值为
(用等体积法或者空间向量等方法同样给分)

练习册系列答案
相关题目

 ,求x的值;
,求x的值; 对于
对于 恒成立,求实数m的取值范围.
恒成立,求实数m的取值范围.  :
: 的离心率为
的离心率为 ,过坐标原点
,过坐标原点 且斜率为
且斜率为 的直线
的直线 与
与 、
、 ,
, .
. 、
、 的值;
的值; 与椭圆
与椭圆 的取值范围.
的取值范围. ,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图).
,AB=BC=2AD=4,E、F分别是AB、CD上的点,EF∥BC,AE = x,G是BC的中点.沿EF将梯形ABCD翻折,使平面AEFD⊥平面EBCF
(如图). ,
,
