题目内容
6.已知点A(1,4),B(3,1),直线l:y=ax+2与线段AB相交于P,求a的取值范围.分析 根据直线斜率公式,进行求解即可得到结论.
解答  解:作出对应的图象如图:
解:作出对应的图象如图:
若直线L:y=ax+2与线段AB相交于P,
直线y=ax+2过定点C(0,2),
则满足kCB≤kCp≤kCA,
∵kCB=$\frac{1-2}{4-0}$=-$\frac{1}{4}$,kCA=$\frac{4-2}{1-0}$=2,
即-$\frac{1}{4}$≤kCp≤2,
即-$\frac{1}{4}$≤a≤2,
故答案为:[-$\frac{1}{4}$,2].
点评 本题主要考查直线方程和直线斜率的应用,利用数形结合是解决本题的关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.函数f(x)=lg$\frac{1+x}{1-x}$(其中x≠±1)是( )函数.
| A. | 奇 | B. | 偶 | C. | 既奇又偶 | D. | 非奇非偶 |
17.将一颗骰子投掷两次得到的点数分别为a,b,则函数f(x)=ax3+bx2+x存在极值的概率为( )
| A. | $\frac{1}{2}$ | B. | $\frac{5}{9}$ | C. | $\frac{7}{12}$ | D. | $\frac{2}{3}$ |
 如图,在正方体ABCD-A1B1C1D1中,找出二面角D1-BC-D的平面角.
如图,在正方体ABCD-A1B1C1D1中,找出二面角D1-BC-D的平面角.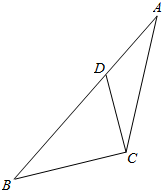 如图,在△ABC中,已知点D在AB边上,且$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,sin∠ACB=$\frac{5\sqrt{7}}{14}$,AC=$\sqrt{7}$,AD=1.
如图,在△ABC中,已知点D在AB边上,且$\overrightarrow{CB}$•$\overrightarrow{CD}$=0,sin∠ACB=$\frac{5\sqrt{7}}{14}$,AC=$\sqrt{7}$,AD=1.