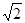题目内容
已知A、B两岛与灯塔C的距离都等于a （km），A岛在灯塔C北偏东15°，B岛在灯塔C南偏东45°，则A、B两岛之间的距离为分析：根据题意画出相应的图形，如图所示，根据平角的定义，由已知的15°和45°，求出∠ACB的度数，在三角形ABC中，再由|AC|=|BC|=a，利用余弦定理即可表示出|AB|的值．
解答：
解：根据图形可知∠ACB=120°，
在△ABC中，|AC|=|BC|=a，
根据余弦定理得：|AB|2=a2+a2-2a•acos120°=3a2，
所以|AB|=
a（km）．
故答案为：
a
解：根据图形可知∠ACB=120°，在△ABC中，|AC|=|BC|=a，
根据余弦定理得：|AB|2=a2+a2-2a•acos120°=3a2，
所以|AB|=
| 3 |
故答案为：
| 3 |
点评：此题属于解直角三角形的题型，涉及的知识有方位角的画法，余弦定理，利用了数形结合的思想，解答此类题的关键是审清题意，画出相应的图形，利用余弦定理建立已知与未知间的关系，从而达到解决问题的目的．
练习册系列答案
相关题目
，灯塔A在岛C的北偏东
，灯塔B在岛C的南偏东
，则灯塔A与灯塔B的距离为（ ）
