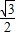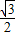题目内容
化简cos15°cos45°-cos75°sin45°的值为( )A.

B.
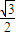
C.-

D.-
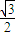
【答案】分析:先利用诱导公式把cos75°转化为sin15°,进而利用两角和的余弦函数求得答案.
解答:解:cos15°cos45°-cos75°sin45°
=cos15°cos45°-sin15°sin45°
=cos(15°+45°)=cos60°=
故选A.
点评:本题主要考查了两角和与差的正弦函数和诱导公式的运用,利用诱导公式把cos75°转化为sin15°关键.属于基础题.
解答:解:cos15°cos45°-cos75°sin45°
=cos15°cos45°-sin15°sin45°
=cos(15°+45°)=cos60°=

故选A.
点评:本题主要考查了两角和与差的正弦函数和诱导公式的运用,利用诱导公式把cos75°转化为sin15°关键.属于基础题.

练习册系列答案
相关题目