题目内容
大楼共有n层,现每层指派一人,共n个人集中到第k层开会 试问如何确定k,能使各位参加会议人员上、下楼梯所走路程总和最小?(假设相邻两层楼梯长都一样)
解:设相邻两层楼梯长为a,则问题转化为下列和式S的最小值的探求:
S=S(k)=a[1+2+3+???+(k-1)]+a[1+2+???+(n-k )]
=a[k2-(n+1)k+ (n2+n)]
(n2+n)]
目标函数S(k)为k的二次函数,且a>0,
故当n为奇数时,取k= ,S最小;当n为偶数时,取k=
,S最小;当n为偶数时,取k= 或
或 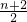 ,S最小.
,S最小.
分析:设相邻两层楼梯长为a,则问题转化为下列和式S的最小值的探求:S=S(k)=a[1+2+3+???+(k-1)]+a[1+2+???+(n-k )],分类讨论,即可得到结论.
点评:本题考查函数的最值,考查学生分析解决问题的能力,正确建模是关键.
S=S(k)=a[1+2+3+???+(k-1)]+a[1+2+???+(n-k )]
=a[k2-(n+1)k+
 (n2+n)]
(n2+n)]目标函数S(k)为k的二次函数,且a>0,
故当n为奇数时,取k=
 ,S最小;当n为偶数时,取k=
,S最小;当n为偶数时,取k= 或
或 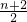 ,S最小.
,S最小.分析:设相邻两层楼梯长为a,则问题转化为下列和式S的最小值的探求:S=S(k)=a[1+2+3+???+(k-1)]+a[1+2+???+(n-k )],分类讨论,即可得到结论.
点评:本题考查函数的最值,考查学生分析解决问题的能力,正确建模是关键.

练习册系列答案
相关题目