题目内容
已知椭圆的一个顶点为A(0,-1),焦点在x轴上.若右焦点到直线 的距离为3.
的距离为3.(1)求椭圆的方程;
(2)设椭圆与直线y=kx+m(k≠0)相交于不同的两点M、N.当|AM|=|AN|时,求m的取值范围.
【答案】分析:(1)依题意可设椭圆方程为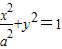 ,由题设
,由题设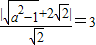 解得a2=3,故所求椭圆的方程为
解得a2=3,故所求椭圆的方程为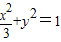 .
.
(2)设P为弦MN的中点,由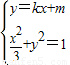 得(3k2+1)x2+6mkx+3(m2-1)=0,由于直线与椭圆有两个交点,∴△>0,即m2<3k2+1.由此可推导出m的取值范围.
得(3k2+1)x2+6mkx+3(m2-1)=0,由于直线与椭圆有两个交点,∴△>0,即m2<3k2+1.由此可推导出m的取值范围.
解答:解:(1)依题意可设椭圆方程为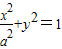 ,
,
则右焦点F(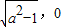 )由题设
)由题设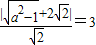
解得a2=3故所求椭圆的方程为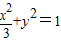 ;
;
(2)设P为弦MN的中点,由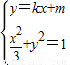
得(3k2+1)x2+6mkx+3(m2-1)=0
由于直线与椭圆有两个交点,∴△>0,即m2<3k2+1①
∴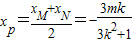 从而
从而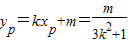
∴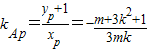 又|AM|=||AN|,∴AP⊥MN,
又|AM|=||AN|,∴AP⊥MN,
则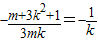 即2m=3k2+1②
即2m=3k2+1②
把②代入①得2m>m2解得0<m<2由②得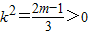 解得
解得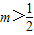 .
.
故所求m的取范围是(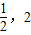 ).
).
点评:本题考查直线与椭圆的位置关系,解题时要认真审题,仔细解答.
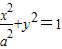 ,由题设
,由题设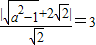 解得a2=3,故所求椭圆的方程为
解得a2=3,故所求椭圆的方程为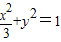 .
.(2)设P为弦MN的中点,由
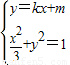 得(3k2+1)x2+6mkx+3(m2-1)=0,由于直线与椭圆有两个交点,∴△>0,即m2<3k2+1.由此可推导出m的取值范围.
得(3k2+1)x2+6mkx+3(m2-1)=0,由于直线与椭圆有两个交点,∴△>0,即m2<3k2+1.由此可推导出m的取值范围.解答:解:(1)依题意可设椭圆方程为
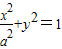 ,
,则右焦点F(
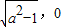 )由题设
)由题设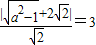
解得a2=3故所求椭圆的方程为
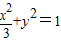 ;
;(2)设P为弦MN的中点,由
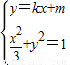
得(3k2+1)x2+6mkx+3(m2-1)=0
由于直线与椭圆有两个交点,∴△>0,即m2<3k2+1①
∴
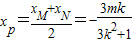 从而
从而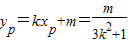
∴
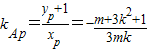 又|AM|=||AN|,∴AP⊥MN,
又|AM|=||AN|,∴AP⊥MN,则
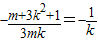 即2m=3k2+1②
即2m=3k2+1②把②代入①得2m>m2解得0<m<2由②得
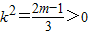 解得
解得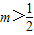 .
.故所求m的取范围是(
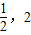 ).
).点评:本题考查直线与椭圆的位置关系,解题时要认真审题,仔细解答.

练习册系列答案
 优质课堂快乐成长系列答案
优质课堂快乐成长系列答案
相关题目
 已知椭圆的一个顶点为A(0,-1),焦点在x轴上,且右焦点到直线x-y+2
已知椭圆的一个顶点为A(0,-1),焦点在x轴上,且右焦点到直线x-y+2