题目内容
(1)请写出一个各项均为实数且公比0<q<1的等比数列,使得其同时满足a1+a6=11且a3•a4=| 32 |
| 9 |
(2)在符合(1)条件的数列中,能否找到一正偶数m,使得am,
| a | 2 m |
| 1 |
| 9 |
分析:(1)根据a1•a6=a3•a4,可知a1,a6应该是方程x2-11x+
=0的两个根,进而求出q和a1的值,得到通项公式;
(2)由am,
, -
成等差数列得出2
=am-
,再由(1)得出m的值.
| 32 |
| 9 |
(2)由am,
| a | 2 m |
| 1 |
| 9 |
| a | 2 m |
| 1 |
| 9 |
解答:解:(1)由条件可知a1,a6应该是方程x2-11x+
=0的两个根,
解得
或
,继而得到q=2或q=
,(4分)
所以符合条件的等比数列可以是an=
•2n-1(公比q>1舍去),(3分)
或an=
•(
)n-1=
•26-n(n∈N*),符合条件(3分)
(2)对于an=
•(
)n-1=
•26-n(3),
由2
=am-
,(2分)
解得m=6.(2分)
| 32 |
| 9 |
解得
|
|
| 1 |
| 2 |
所以符合条件的等比数列可以是an=
| 1 |
| 3 |
或an=
| 32 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
(2)对于an=
| 32 |
| 3 |
| 1 |
| 2 |
| 1 |
| 3 |
由2
| a | 2 m |
| 1 |
| 9 |
解得m=6.(2分)
点评:本题考查了等差数列的性质以及等比数列的通项公式,要注意公比0<q<1的,属于中档题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
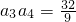 ;
;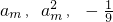 这三个数依次成等差数列?若能,求出这个m的值; 若不能,请说明理由.
这三个数依次成等差数列?若能,求出这个m的值; 若不能,请说明理由.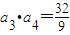 ;
;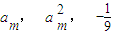 这三个数依次成等差数列?若能,求出这个m的值; 若不能,请说明理由.
这三个数依次成等差数列?若能,求出这个m的值; 若不能,请说明理由.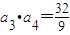 ;
;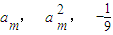 这三个数依次成等差数列?若能,求出这个m的值; 若不能,请说明理由.
这三个数依次成等差数列?若能,求出这个m的值; 若不能,请说明理由.