题目内容
若sin(
x+
)=
,x∈(-2,2),则x=
| π |
| 2 |
| π |
| 4 |
| ||
| 2 |
0或1
0或1
.分析:设u=sinv,由x的范围,求出
x+
的范围,并设v=
x+
,且由u=sinv,根据题意画出图形,根据图形及sin(
x+
)的值,列出关于x的方程,求出方程的解即可得到x的值.
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
解答:解:∵x∈(-2,2),
∴设v=
x+
∈(-
,
),
设u=sinv,根据题意画出图形,如图所示:
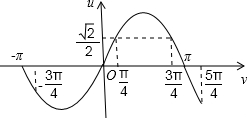
根据图形可得:
x+
=
或
x+
=
,
解得:x=0或x=1,
则x=0或1.
故答案为:0或1
∴设v=
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
| 5π |
| 4 |
设u=sinv,根据题意画出图形,如图所示:

根据图形可得:
| π |
| 2 |
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
| 3π |
| 4 |
解得:x=0或x=1,
则x=0或1.
故答案为:0或1
点评:此题考查了三角函数的化简求值,涉及的知识有正弦函数的图象与性质,以及特殊角的三角函数值,利用了数形结合的思想,根据x的范围求出所求式子角的范围,画出相应的图形是解本题的关键.

练习册系列答案
相关题目