题目内容
设函数f(x)=xsinx,x∈[-
,
],若f(x1)>f(x2),则下列不等式一定成立的是( )
| π |
| 2 |
| π |
| 2 |
分析:由f(-x)=-x•sin(-x)=f(x)⇒f(x)=xsinx为偶函数,f′(x)=sinx+xcosx,当x∈[0,
]⇒f′(x)>0⇒f(x)单调递增,
⇒x∈[-
,0]时,f(x)单调递减;于是f(x1)>f(x2)?|x1|>|x2|?x12>x22,问题解决了.
| π |
| 2 |
⇒x∈[-
| π |
| 2 |
解答:解:∵f(-x)=-x•sin(-x)=xsinx=f(x),
∴函数f(x)=xsinx为偶函数,又f′(x)=sinx+xcosx,
∴x∈[0,
]时,f′(x)≥0,f(x)单调递增,x∈[-
,0]时,f′(x)≤0,f(x)单调递减;
∴f(x1)>f(x2)?f(|x1|)>f(|x2|)?|x1|>|x2|?x12>x22,
故选B.
∴函数f(x)=xsinx为偶函数,又f′(x)=sinx+xcosx,
∴x∈[0,
| π |
| 2 |
| π |
| 2 |
∴f(x1)>f(x2)?f(|x1|)>f(|x2|)?|x1|>|x2|?x12>x22,
故选B.
点评:本题考查函数单调性的判断与证明,难点在于“f(x)=xsinx在x∈[0,
]时f(x)单调递增”的证明(导数法)及偶函数性质的综合应用(f(x1)>f(x2)?|x1|>|x2|),属于难题.
| π |
| 2 |

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目
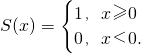 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x). 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x). 例如要表示分段函数
例如要表示分段函数 可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).
可以将g(x)表示为g(x)=xS(x-2)+(-x)S(2-x).