题目内容
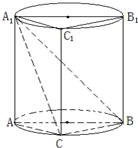
如图组合体中,三棱柱ABC-A1B1C1的侧面ABB1A1是圆柱的轴截面,C是圆柱底面圆周上不与A,B重合一个点.
(1)求证:无论点C如何运动,平面A1BC⊥平面A1AC;
(2)当C是弧AB的中点时,求四棱锥A1-BCC1B1与圆柱的体积比.
(1)求证:无论点C如何运动,平面A1BC⊥平面A1AC;
(2)当C是弧AB的中点时,求四棱锥A1-BCC1B1与圆柱的体积比.

(I)因为侧面ABB1A1是圆柱的轴截面,C是圆柱底面圆周上不与A,B重合一个点,所以AC⊥BC(2分)
又圆柱母线AA1⊥平面ABC,BC属于平面ABC,所以AA1⊥BC,
又AA1∩AC=A,所以BC⊥平面A1AC,
因为BC?平面A1BC,所以平面A1BC⊥平面A1AC;(6分)
(II)设圆柱的底面半径为r,母线长度为h,
当点C是弧
的中点时,三角形ABC的面积为r2,
三棱柱ABC-A1B1C1的体积为r2h,
三棱锥A1-ABC的体积为
r2h,
四棱锥A1-BCC1B1的体积为r2h-
r2h=
r2h,(10分)
圆柱的体积为πr2h,
四棱锥A1-BCC1B1与圆柱的体积比为2:3π.(12分)

又圆柱母线AA1⊥平面ABC,BC属于平面ABC,所以AA1⊥BC,
又AA1∩AC=A,所以BC⊥平面A1AC,
因为BC?平面A1BC,所以平面A1BC⊥平面A1AC;(6分)
(II)设圆柱的底面半径为r,母线长度为h,
当点C是弧
 |
| AB |
三棱柱ABC-A1B1C1的体积为r2h,
三棱锥A1-ABC的体积为
| 1 |
| 3 |
四棱锥A1-BCC1B1的体积为r2h-
| 1 |
| 3 |
| 2 |
| 3 |
圆柱的体积为πr2h,
四棱锥A1-BCC1B1与圆柱的体积比为2:3π.(12分)

练习册系列答案
 口算题卡北京妇女儿童出版社系列答案
口算题卡北京妇女儿童出版社系列答案
相关题目
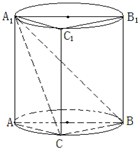 如图组合体中,三棱柱ABC-A1B1C1的侧面ABB1A1是圆柱的轴截面,C是圆柱底面圆周上不与A,B重合一个点.
如图组合体中,三棱柱ABC-A1B1C1的侧面ABB1A1是圆柱的轴截面,C是圆柱底面圆周上不与A,B重合一个点.
 (Ⅱ)当点
(Ⅱ)当点 如图组合体中,三棱柱ABC-A1B1C1的侧面ABB1A1是圆柱的轴截面,C是圆柱底面圆周上不与A,B重合一个点.
如图组合体中,三棱柱ABC-A1B1C1的侧面ABB1A1是圆柱的轴截面,C是圆柱底面圆周上不与A,B重合一个点. 如图组合体中,三棱柱ABC-A1B1C1的侧面ABB1A1是圆柱的轴截面,C是圆柱底面圆周上不与A,B重合一个点.
如图组合体中,三棱柱ABC-A1B1C1的侧面ABB1A1是圆柱的轴截面,C是圆柱底面圆周上不与A,B重合一个点.