题目内容
(2012•广东模拟)函数y=log2
的图象( )
| 1+x |
| 1-x |
分析:先求函数的定义域,再利用函数奇偶性的定义,证明函数f(-x)=-f(x),即可证明此函数为奇函数,从而其图象关于原点对称
解答:解:函数f(x)=y=log2
的定义域为(-1,1),
且f(-x)=log2
=-log2
=-f(x)
∴函数f(x)为定义域上的奇函数,其图象关于原点对称
故选 A
| 1+x |
| 1-x |
且f(-x)=log2
| 1-x |
| 1+x |
| 1+x |
| 1-x |
∴函数f(x)为定义域上的奇函数,其图象关于原点对称
故选 A
点评:本题主要考查了函数奇偶性的定义及其判断方法,奇函数的图象性质,证明函数为奇函数是解决本题的关键,属基础题

练习册系列答案
相关题目
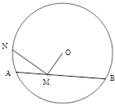 (2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=
(2012•广东模拟)(几何证明选讲选做题)如图,点M为⊙O的弦AB上的一点,连接MO.MN⊥OM,MN交圆于N,若MA=2,MB=4,则MN=