题目内容
17．当x∈（0，3）时，关于x的不等式ex-x-2mx＞0恒成立，则实数m的取值范围是（ ）| A． | （-∞，$\frac{e-1}{2}$） | B． | （$\frac{e-1}{2}$，+∞） | C． | （-∞，e+1） | D． | （e+1，+∞） |
分析 由题意可得2m+1＜$\frac{{e}^{x}}{x}$在（0，3）的最小值，求出f（x）=$\frac{{e}^{x}}{x}$的导数和单调区间，可得f（x）的最小值，解不等式即可得到m的范围．
解答 解：当x∈（0，3）时，关于x的不等式ex-x-2mx＞0恒成立，
即为2m+1＜$\frac{{e}^{x}}{x}$在（0，3）的最小值，
由f（x）=$\frac{{e}^{x}}{x}$的导数为f′（x）=$\frac{{e}^{x}（x-1）}{{x}^{2}}$，
当0＜x＜1时，f′（x）＜0，f（x）递减；
当1＜x＜3时，f′（x）＞0，f（x）递增．
可得f（x）在x=1处取得最小值e，
即有2m+1＜e，
可得m＜$\frac{e-1}{2}$．
故选：A．
点评 本题考查不等式恒成立问题的解法，注意运用参数分离和构造函数法，运用导数求出单调区间和最值，考查运算能力，属于中档题．
练习册系列答案
相关题目
7．为了调查高中学生是否喜欢数学与性别的关系，随机抽查男、女学生各 40 名，得到具体数据如表：
（I）根据上面的列联表，能否在犯错误的概率不超过 0.025 的前提下，认为是否喜欢数学与性别有关？
（II）计算这 80 位学生不喜欢数学的频率；（III）用分层抽样的方法从不喜欢数学的男女学生中抽查 6 人进行数学问卷调查，再从中抽取 4 份问卷递交校长办，求至少抽出 3 名女生问卷的概率．
参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
参考数据：
| 是否喜欢数学 | 是 | 否 | 合计 |
| 男生 | 30 | 10 | 40 |
| 女生 | 20 | 20 | 40 |
| 合计 | 50 | 30 | 80 |
（II）计算这 80 位学生不喜欢数学的频率；（III）用分层抽样的方法从不喜欢数学的男女学生中抽查 6 人进行数学问卷调查，再从中抽取 4 份问卷递交校长办，求至少抽出 3 名女生问卷的概率．
参考公式：${K^2}=\frac{{n{{（ad-bc）}^2}}}{（a+b）（c+d）（a+c）（b+d）}$，其中n=a+b+c+d．
参考数据：
| P（K2≥k0） | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| k0[来源：] | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
8．已知平面α和两条直线a，b，则下列结论成立的是（ ）
| A． | 如果a∥α，b∥α，那么a∥b | |
| B． | 如果a∥b，a∥α，b?α，那么b∥α | |
| C． | 如果a∥b，那么α平行于经过b的任何平面 | |
| D． | 如果a∥α，那么a与α内的任何直线平行 |
12．
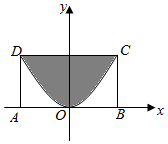如图，设不等式组$\left\{{\begin{array}{l}{-1≤x≤1}\\{0≤y≤1}\end{array}}\right.$表示的平面区域为长方形ABCD，长方形ABCD内的曲线为抛物线y=x2的一部分，若在长方形ABCD内随机取一个点，则此点取自阴影部分的概率等于（ ）
如图，设不等式组$\left\{{\begin{array}{l}{-1≤x≤1}\\{0≤y≤1}\end{array}}\right.$表示的平面区域为长方形ABCD，长方形ABCD内的曲线为抛物线y=x2的一部分，若在长方形ABCD内随机取一个点，则此点取自阴影部分的概率等于（ ）| A． | $\frac{2}{3}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{1}{4}$ |
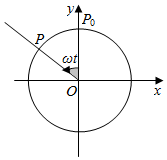如图，点P是半径为1的砂轮边缘上的一个质点，它从初始位置P0开始，按逆时针方向以角速度ω=1rad/s做圆周运动，记点P的纵坐标y关于时间t（t≥0，t的单位：s）的函数关系为y=f（t）．